📚선형 회귀
선형 회귀는 파라미터가 선형 값인 모델이다. 독립변수가 n차 이더라도 파라미터가 1차이면 선형 함수이다.

따라서 위 두 개의 식 모두 선형 회귀이다. 계수에 루트나 n차 분수가 들어가도 선형 회귀이다.

하지만 파라미터가 n차로 올라가면 비선형 모델이 된다.


위의 식은 모델에 대해서 샘플이 10개일 때, MSE 비용함수를 식으로 나타낸 것이다. 식을 정리해보면 비용함수는 최종적으로 파라미터(b0, b1)에 대한 함수임을 알 수 있다. 이 비용함수를 최소화하는 방법에는 앞선 포스트에서 작성한 것처럼 (1) Normal Equation (2) 경사하강법 두 가지가 있다.
✅ 정규방정식(Normal Equation) vs 행렬로 풀기
선형회귀 모델의 최적 파라미터 값을 구할 때 정규방정식을 사용하는 방법과 행렬로 푸는 방법을 비교해보자.
📌 예시


위의 예제에서는 데이터 샘플이 2개이고 주어진 모델을 바탕으로 회귀 문제를 풀어야 한다.
E는 MSE비용함수를 나타낸다. 최적의 파라미터 조합을 찾기 위해서는 아래 두 개의 식을 동시에 만족하는 b1, b2를 구해야 한다.
📌 Normal Equation 으로 풀기
구해야 하는 파라미터가 2개 이상이기 때문에 대입법/소거법을 이용해서 연립방정식을 풀어야 한다.

최적 b1, b2 값을 구하기 위해서는 위의 각 식을 만족하는 값을 구해야 한다

전체 E는 위와 같고, b1 b2 각각에 대해서 미분을 하면


대입법과 소거법을 이용해서 위와 같이 b1, b2 값을 구할 수 있다. 하지만 파라미터가 너무 많아지면 이 방식으로 계산이 불가능해진다.
📌 행렬을 이용해서 풀기


위 모델에서 y1, y2는 위와 같이 식으로 표현할 수 있다. 이를 행렬로 표현하면

위와 같이 행렬 연산으로 간단하게 표현할 수 있다. X 행렬에서 1열은 X1에 대한 정보를, 2열은 X2에 대한 정보를 담고 있다.

전체 error vector는 위와 같이 나타낼 수 있다.

각 e에 대해서 MSE를 위와 같이 나타낼 수 있다. 아래 1/N은 최고값에 영향을 미치지 않기 때문에 생략하고 작성한다.

이 예제에서는 샘플이 2개 이므로 e1, e2를 사용해서 비용함수를 풀어서 쓸 수 있다.
이 식을 행렬로 나타내기 위해서는 전치행렬의 내적을 사용한다.

행렬을 이용해서 비용함수를 eTe 로로 표현할 수 있다.
다음 단계에서는 비용함수를 최소화하는 b 벡터의 값을 찾아야 한다. b는 b1, b2로 구성된 파라미터 벡터이다.

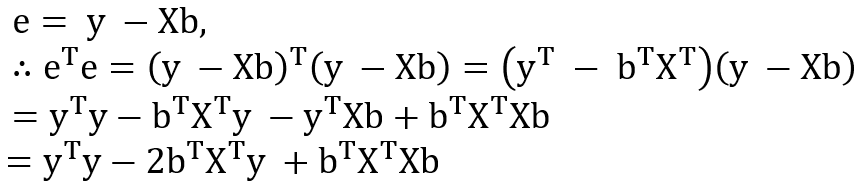
e = y-Xb 이고 행렬 전치 공식에 따라서 식을 전개하면 위와 같다. 마지막 줄이 비용함수를 나타내는 식이라는 것을 잊지 말기.
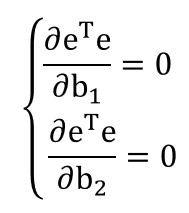
따라서 eTe = E 에 대해서 위의 식을 만족하는 b1, b2 값을 찾아야 한다. 여기서 eTe는 하나의 스칼라 값이다.
🏷️참고 : 벡터에 대한 미분 표현
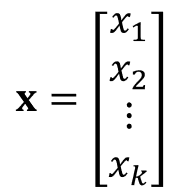
다음과 같은 벡터 x가 있을 때
y가 스칼라인 경우, 아래와 같이 표현이 가능하다
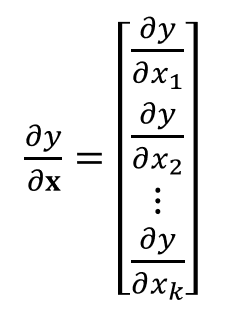
벡터에 대한 미분 표현을 이용하여, 위의 eTe에 대한 식을 전개하면
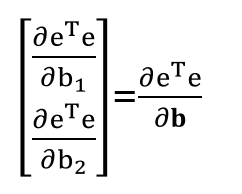
eTe는 하나의 스칼라 값이고, b = [b1, b2] 인 벡터이기 때문에 역 방향으로 식을 정리할 수 있다.
이제 이 식에 대해서 normal equation 방식으로 b1, b2를 구할 수 있다. 이를 위해서는 아래 방정식을 풀어야 한다.
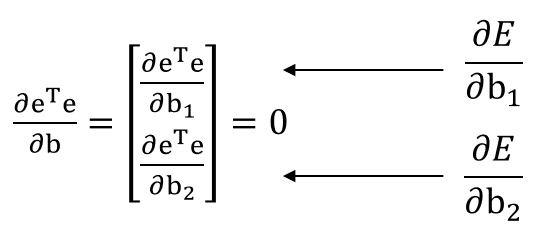
🏷️ 참고 : 벡터 미분 공식
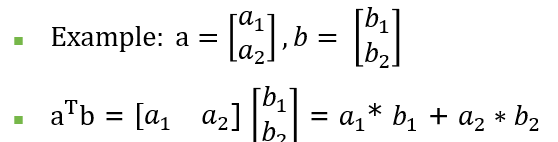
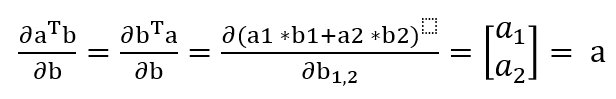
위와 같이 나타낼 수 있다. 여기서 분자는 모두 스칼라이다.
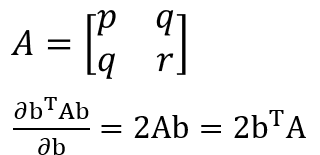
또한 A와 같이 정사각 대칭행렬이 있을 때, 미분 공식으로 위와 같이 나타낼 수 있다. 여기서도 분자는 스칼라이다.
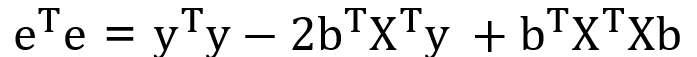
앞서 선개한 위의 식에서 XTX는 정사각 대칭 행렬이므로
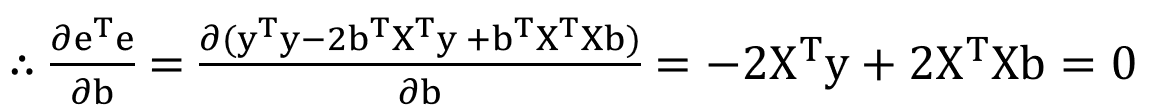
첫 번째 항은 상수여서 사라지고, 두 번째 항과 세 번째 항에 대해서 앞서 정리한 미분 공식을 사용하면 위와 같이 나타낼 수 있다.

좌변과 우변을 정리하고 최종적으로 파라미터 벡터인 b에 대한 식으로 나타낼 수 있다. 이 공식은 독립변수의 수와 상관없이 행렬로 나타낼 수 있다. 즉 위의 b는 최적 파라미터 값으로 구성된 파라미터 벡터이다.
📌 예시
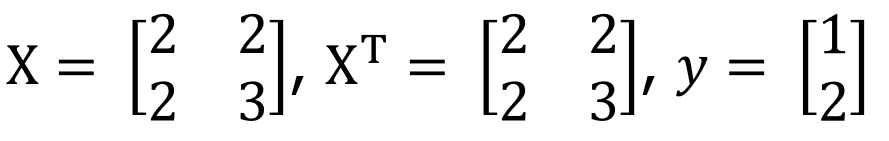
위와 같이 값이 주어질 때 이에 대해서 최적 파라미터를 파이썬으로 계산하면
import numpy as np
X = np.array([[2,2],
[2,3]])
y = np.array([[1],
[2]])
b = np.dot(np.linalg.inv(np.dot(X.T, X)),np.dot(X.T,y))
b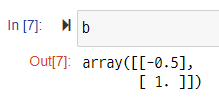
방정식을 풀이한 것과 동일한 결과를 얻을 수 있다.
📌 역행렬이 존재하지 않는 경우?
위 식에서 역행렬 계산은 넘파이의 np.linalg.inv()를 사용한다.
하지만 행렬이 Full Rank가 아닌 경우, 행렬식 = 0, 고유값 = 0 인 경우에는 역행렬이 존재하지 않는다.
이런 경우에는 Pseudo inverse 개념을 사용해서 np.linalg,pinv()를 사용한다.
이 함수는 역행렬이 존재하면 기존 np.linalg.inv() 함수와 동일한 결과를 리턴하고, 역행렬이 존재하지 않을 때만 가짜 역행렬을 반환해주기 때문에 대부분 이 함수를 사용한다.
📚 모델의 성능 평가하기

R2 : 모델의 설명력. 종속변수를 설명하는 정도라고 해석할 수도 있다.
종속변수의 전체 흩어진 정도 / 모델이 설명하는 정도
1에 가까울수록 데이터에 대한 모델의 설명력이 좋은것
📚 Feature Scaling
독립변수들은 단위가 모두 다르기 때문에, 단위가 큰 독립변수는 분산이 크기 때문에 종속변수에 대한 설명력이 커지는 상황이 발생할 수 있다.
ex) 독립변수 : 경력(year), 몸무게(kg)
종속변수 : 연봉
위와 같은 경우에 실제 연봉에 미치는 영향은 경력 변수가 크지만, 몸무게 변수의 분산이 크기 때문에 모델에서 설명력이 크게 나타날 수 있다. 이는 새로운 데이터에 대한 예측력을 저하시킨다.
📌 1. 표준화 (Standardization)
평균=0, 분산=1 인 분포로 변경
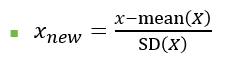
📌2. Min-Max normalization
최대값=1, 최소값=0 인 상태로 변경
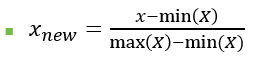
위의 두 스케일링 방법 중에서 어떤 것이 주어진 데이터에 적합한 지는 해봐야 알 수 있다. 두 가지 방법을 모두 시도해보고 성능이 좋은 방식을 선택하면 됨. 또한 스케일링이 반드시 모델 성능을 향상시키는 것이 아니기 때문에 기본 변수로도 모델 학습을 진행해 봐야한다.
📌스케일링 시 주의해야 할 점 !

train set과 test set을 별도로 스케일링 해서는 안된다. 즉, 학습 데이터에서 얻어진 평균과 표준편차로 평가 데이터에 대해서도 스케일링을 실시해야 한다. 학습 데이터로 fit_transform을 실시하고 평가 데이터에 대해서는 transform만 진행한다. 별도로 스케일링을 하게되면 동일한 값을 가지는 관측치가 스케일링 이후에 값이 달라진다. 이렇게 되면 학습 데이터로 학습한 모델의 성능을 평가 데이터로 올바르게 파악할 수 없다.
추가) train/test 분리 전에 전체 변수를 스케일링 하면 안 됨 → train 데이터에 test 데이터의 정보가 반영 됨
📚 Lasso vs Ridge
선형 회귀에 L1 규제를 적용한 것을 Lasso Regression ( https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html),
L2 규제를 적용한 것을 Ridge Regression ( https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html) 이라고 한다.
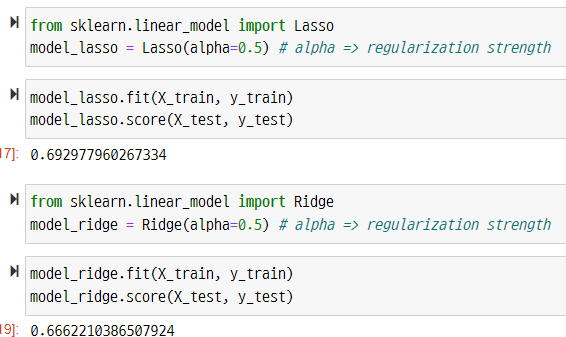
위 코드에서 alpha 는 패널티의 정도를 나타내는 람다를 의미한다.
값이 클수록 패널티를 강하게 준다는 것을 의미한다. L1 규제의 경우 변수의 파라미터 값이 0이 될수도 있다.
L1과 L2 규제를 섞어서 사용한 방식을 Elastic net이라고 한다.
📚 Reference
이상엽, 연세대학교 언론홍보영상학부 부교수, 22년도 1학기 기계학습 이론과 실습
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 군집화(Clustering) (0) | 2022.03.28 |
|---|---|
| [머신러닝] 데이터 전처리 (2) | 2022.03.21 |
| [머신러닝] 지도학습 / 경사하강법 / 규제화 (0) | 2022.03.07 |
| [머신러닝] 클러스터링(Clustering) (0) | 2021.12.01 |
| [머신러닝] Decision Tree (0) | 2021.10.13 |



댓글