◈ Decision Tree 개념
가장 기본적이면서 직관적인 알고리즘이지만, 최근 머신러닝 문제에 자주 사용되는 여러 부스팅 계열 알고리즘의 기본이 된다.
• Recursive Partitioning :
트리에서 branch를 최대한 많이 만들어서 maximum homogeneity를 달성한다.
즉 데이터의 상태가 최대한 pure 한 상태가 되도록 가지를 생성함 (이진 분류인 경우 한쪽 클래스로만 분류되도록)
Pruning Tree : branch가 너무 많을 경우 과적합이 발생할 수 있으므로, pruning을 실시한다.



• Riding mower 사례에서, 좌측처럼 2개의 변수로 분류를 실시할 때, 우측처럼 데이터를 최대한 pure한 상태(이질성이 적은 상태)로 분류하는게 최선의 트리이다.
✅ Impurity Measures
① Gini Index

- P : proportion of cases in rectangle A that belong to class k (out of m classes)
- l(A) : when all cases belong to same class
- Max Value : 두 개의 클래스가 반반 있을 때의 값인 0.5,
Min Value : 0
→ 지니 계수 값이 낮을수록 좋은 것

- 두 개의 클래스가 반반으로 똑같이 섞여있으면 0.5로 계산되고, 이것이 지니계수의 최대값이다.
자식 노드에서 불순도가 0.359로 감소한 것을 확인할 수 있음
② Entropy

• P : proportion of cases in rectangle A that belong to class k (out of m classes)
• 가장 불순도가 높을 때 1로 나타나고, 낮을수록 좋은 값
• child node 전체의 엔트로피 값은 각 노드로 분류될 확률에 지니계수를 가중치로 곱해서 계산한다.
③ Information Gain Ratio
• Information Gain : 1 - 엔트로피 지수
- 자식 노드가 많아지면 자연스럽게 불순도가 낮아진다. 하지만 동시에 모델이 복잡해진다
- 따라서 지나치게 복잡한 구조에 대해서 패널티를 부여하는 것이 information gain
④ Chi-square test
• Pearson's Chi-square Static (x^2 값 이용)

• 대부분의 최근 DT 패키지는 CART 알고리즘을 사용하지만, 과거에 사용된 CHAID는 카이스퀘어 검정을 사용함
→ 즉, node를 생성할 때마다 카이스퀘어 검정을 이용하여 통계적으로 의미가 있는지 확인함
• 특정한 기준으로 split 을 했을 때, 그 split이 의미가 있으려면 분류된 child 노드에서 비율 차이가 유의미하게 나야함
→ Ecpectancy frequency 와 observed frequency 사용
• Ecpectancy frequency는 split에 사용한 기준이 의미가 없어서, 반반 동일하게 나눠지는 상황을 의미함 (용어 혼선 주의)

✅ Pruning
• 가지 수가 많아질수록 과적합 가능성이 증가함.
• spliting 횟수를 파라미터로 설정 가능, 단 임의적/주관적이라는 단점 있음
• fully grown tree 생성 후, 가지를 쳐나가는 방식 (CART 알고리즘에서 이 방식 사용)

- 일반적으로 파라미터를 조정하는 것 보다 성능이 좋음
- a : 낮을수록 가지가 많은 복잡한 형태, 클수록 단순한 형태
- 각 노드에 대해서 해당 노드를 그대로 뒀을 때와 삭제했을 때의 CC(T)를 계산하고 비교해봄.
만약 삭제 했을 때 CC(T) 가 낮아지면 해당 가지의 pruning을 실시함
✅ Tree Instability
• DT의 단점은 학습 데이터에 따라서 분류 기준이 달라질 수 있다는 것이다. 이를 보완하기 위해서 CV 사용

✅ Random Foest
• 여러 트리의 결과를 결합한 앙상블 기법. 단일 트리보다 성능 훨씬 뛰어남
• 단, 단순 트리 모델 보다는 설명력 감소(if-then rule 사용할 수 없음) → 대신, variable importance 사용 가능
• 단계
1) Draw multiple bootstrap resamples of cases from data, with replacement(복원추출)
2) For each resample, use random subset of predictors and produce a tree
3) Combine predictions/classification from all trees
◈ 실습
Universal Bank 데이터셋으로 DT를 이용한 기본적인 분류와 회귀 분석을 진행했다.
✅ 데이터 불러오기
bank.df <- read.csv("UniversalBank.csv", na.strings = "") #기본적인 데이터 구조 살펴보기 str(bank.df) #변수 유형 변경 : interger -> Factor bank.df$Personal.Loan <- factor(bank.df$Personal.Loan) # Drop ID and zip code columns. bank.df <- bank.df[ ,-c(1, 5)]
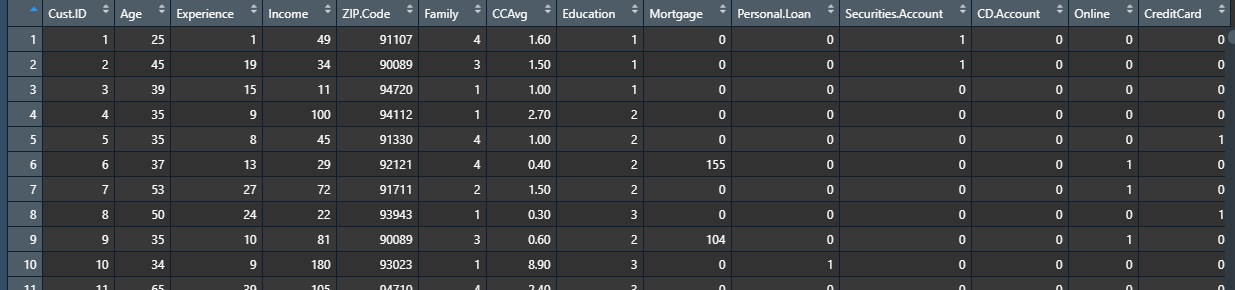
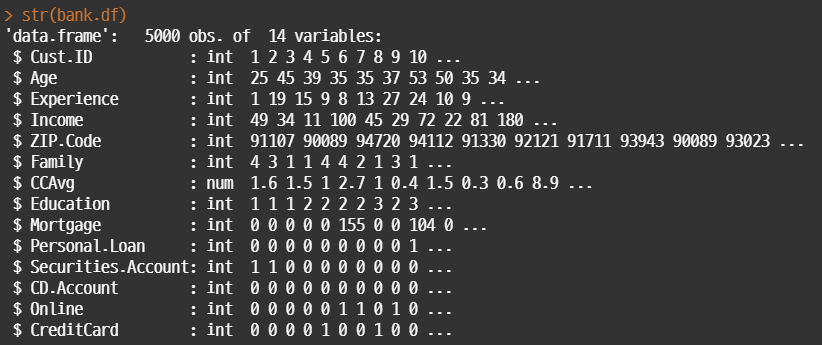
• 기본적인 데이터 구조와 변수 유형 파악. DT는 변수 유형이 크게 중요하지 않지만, R 버전 등에 따라서 오류가 발생하는 경우도 있어서 기본적으로 범주형으로 사용하는 것이 좋다.
✅ DT 학습
# train/test 분리 set.seed(1) train.index <- sample(c(1:dim(bank.df)[1]), dim(bank.df)[1]*0.6) train.df <- bank.df[train.index, ] valid.df <- bank.df[-train.index, ] #라이브러리 사용 library(rpart) library(rpart.plot) #트리 생성 default.ct <- rpart(Personal.Loan ~ ., data = train.df, method = "class") #트리 확인 print(default.ct) rpart.rules(default.ct) #최종 노드 수 확인 length(default.ct$frame$var[default.ct$frame$var == "<leaf>"])

• train, test 데이터를 분리한 후, rpart(recursive partitioning and regression tree)라이브러리를 불러온다.
• 트리 생성시 method='class' 는 classification / method='anova' 는 regression
• 디폴트 impurity 지수는 지니계수 사용함
✅ Confusion Matrix
#caret 패키지 사용 library(caret) #train 데이터 default.ct.point.pred.train <- predict(default.ct, train.df, type = "class") confusionMatrix(default.ct.point.pred.train, train.df$Personal.Loan) #test 데이터 default.ct.point.pred.valid <- predict(default.ct, valid.df, type = "class") confusionMatrix(default.ct.point.pred.valid, valid.df$Personal.Loan)
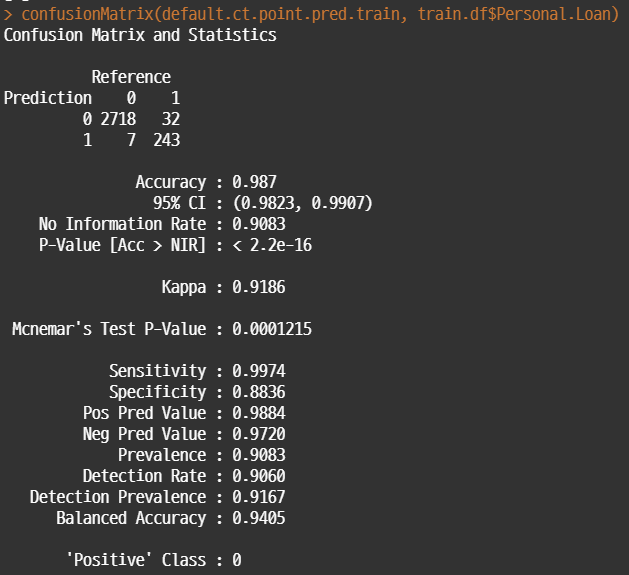
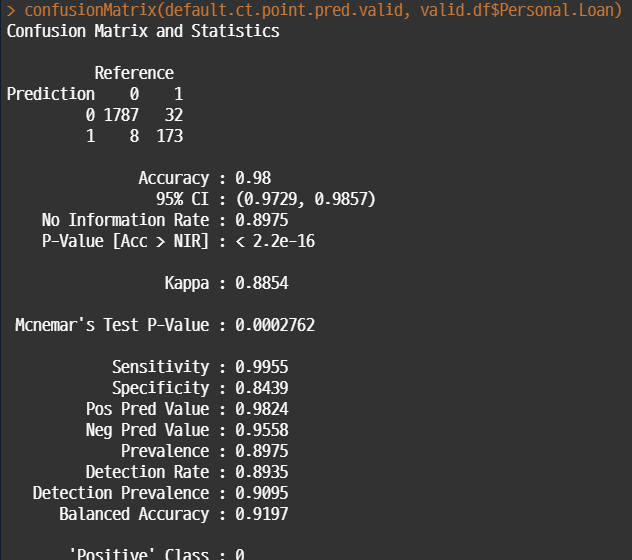
• test / valid 데이터 각각에 대해서 confusion matrix로 성과를 평가해보면 다음과 같다.
✅ 시각화
prp(default.ct, type = 1, extra = 1, under = TRUE, split.font = 1, varlen = -10, box.col=ifelse(default.ct$frame$var == "<leaf>", 'gray', 'white'))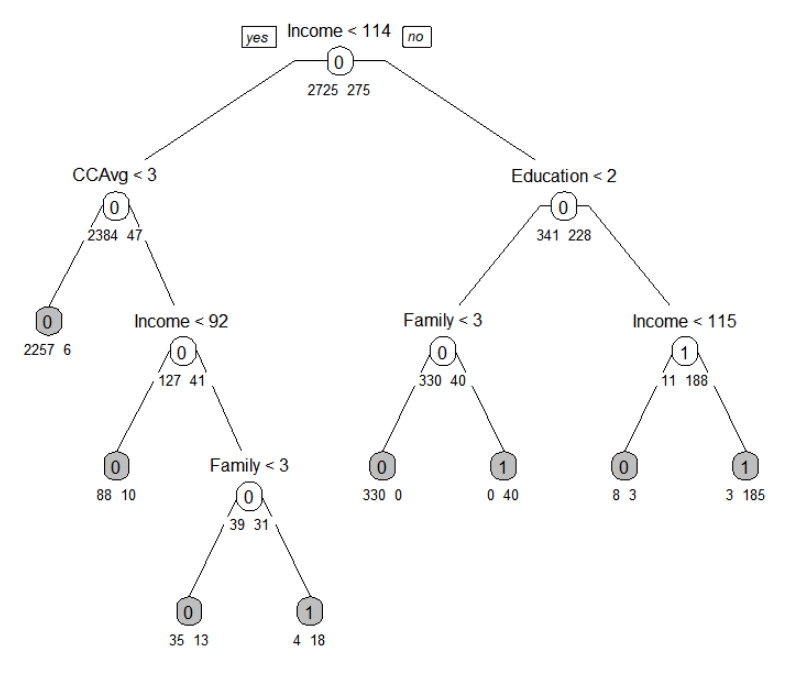
• prp() 를 사용하여 트리 시각화 가능. 시각화 요소에 대한 세부 파라미터는 아래와 같음
## type=0: Display the number of observations that fall in the terminal node only
## extra=1: Display the number of observations that fall in the node, if extra = 0, does not display
## under: if TRUE, display the number of observations under a node.
## under: If FALSE, display inside the node box
## varlen: Length of variable names in text at the splits (default = ‐8)
## varlen: positive value for abbreviation, negatgive for truncating
## split.font: Font size for the split labels. Default 2, bold.
#새로운 데이터 생성 new.df <- data.frame(Age= 55, Experience= 20, Income= 40, Family= 3, CCAvg= 6, Education= 2, Mortgage= 70, Personal.Loan= 1, Securities.Account= 1, CD.Account= 1, Online= 1, CreditCard = 1) # 새로운 값 예측 ## 각 클래스로 분류될 확률 predict(default.ct, new.df) ## 각 클래스 값 predict(default.ct, new.df, type = "class")
• 다른 알고리즘과 동일하게 predict를 이용하여 새로운 데이터에 대한 예측값 출력이 가능하다. type='class'를 추가하면 최종 분류된 클래스만 출력함
✅ 시각화 2
library(RColorBrewer) library(rattle) fancyRpartPlot(default.ct)
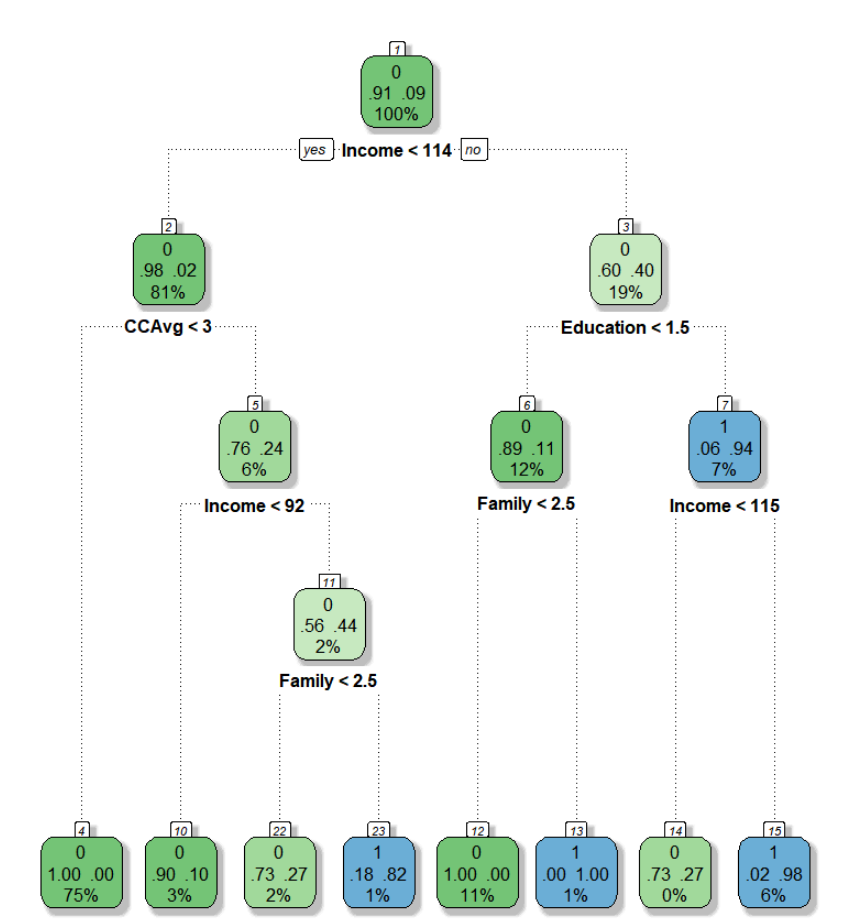
• rattle 패키지를 이용하면 보다 직관적인 시각화가 가능하다. 별도의 파라미터 조절할 필요 없이 이 방식이 제일 깔끔한 듯 하다.
✅ 파라미터 수정
#파라미터 수정 new.ct <- rpart(Personal.Loan ~ ., data = train.df, method = "class", maxdepth = 5, cp=0, minsplit=1, minbucket = 10) #시각화 fancyRpartPlot(new.ct)
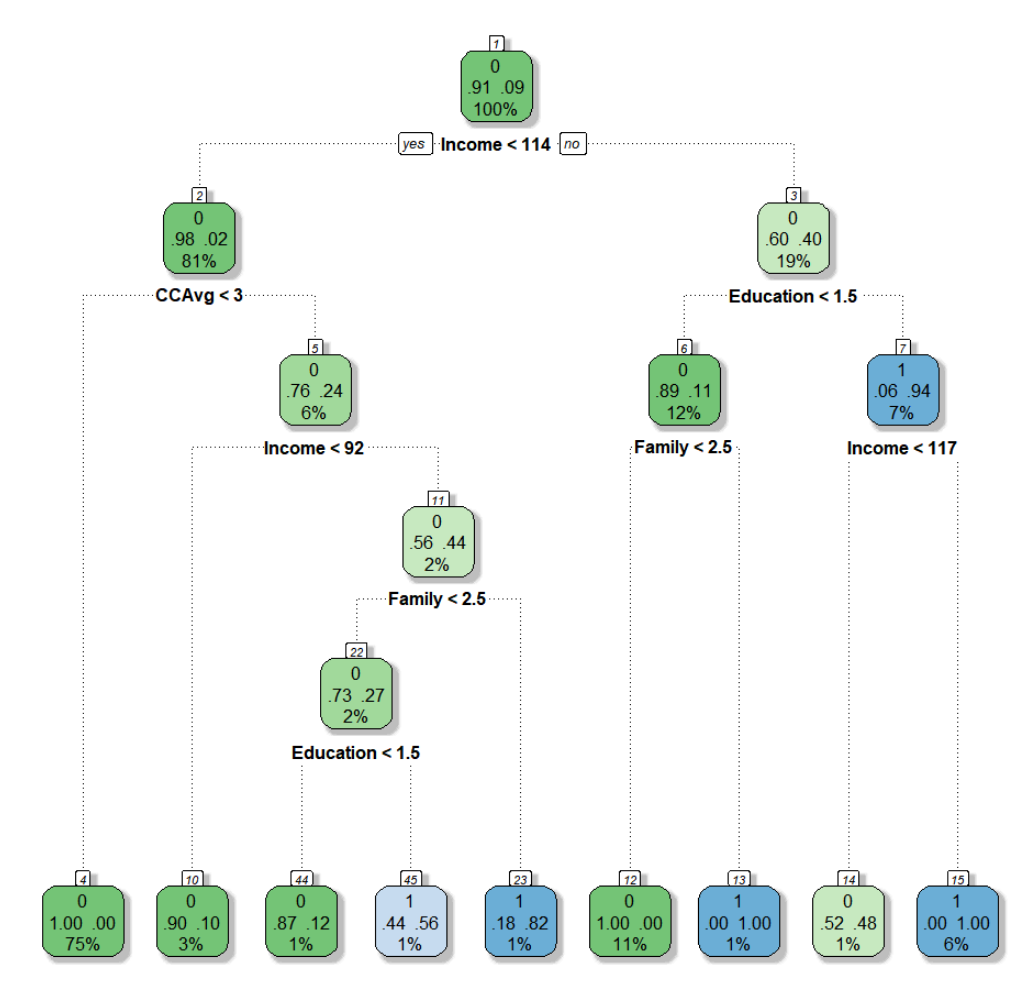
• DT 파라미터 수정해서 트리 최적화가 가능하다. 트리가 깊어질수록 과적합이 발생할 가능성이 높으니 파라미터를 적절하게 조절해야 한다. 주요 파라미터 설명은 다음과 같다.
## cp : maximum depth -> 0일 경우 fully grown
## minsplit : 해당 노드에 속하는 최소한의 데이터 포인트 수
## maxdepth : 최대 깊이
## minbucket : 마지막 노드에 있는 최소한의 숫자
◈ 참고자료 출처
• Data Mining for Business Analytics: Concepts, Techniques, and Application in R" by R, Galit Shmueli, Peter C. Bruce, Inbal Yahav, Nitin R. Patel, Kenneth C. Lichtendahl Jr. Wiley. 1st edition. Wiley, 2017.
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 선형회귀 (Linear Regression) (0) | 2022.03.14 |
|---|---|
| [머신러닝] 지도학습 / 경사하강법 / 규제화 (0) | 2022.03.07 |
| [머신러닝] 클러스터링(Clustering) (0) | 2021.12.01 |
| [머신러닝] Naive Bayes 개념 정리 (0) | 2021.10.08 |
| [머신러닝] KNN 개념 정리 (0) | 2021.10.06 |




댓글