📚 머신러닝이란
머신러닝이란 머신(=컴퓨터)가 주어진 데이터에서 유용한 정보를 추출에서 문제를 해결하기 위해서 사용되는 것을 의미한다. 머신러닝을 위해서 알고리즘이 사용되는데, 알고리즘은 데이터를 학습하기 위한 "수학적인 모형"을 의미한다. 머신러닝 알고리즘은 아래와 같이 3가지로 분류된다.
① 지도학습
• 힌트와 정답 정보를 모두 가진 데이터를 학습해서 정답을 예측하는 학습 방식
② 비지도학습
• 관측치들의 특성 정보를 담고 있는 학습 데이터를 사용해서, 관측치들의 특성 or 패턴을 파악하는 것
• 주로 exploratory analysis 목적으로 사용된다.
③ 강화학습
• 주어진 문제를 해결하기 위해서 일련의 action을 연속적으로 수행하고, 각 행동에 대한 보상과 페널티를 부여해서 원하는 결과를 얻도록 유도한다.
• 컴퓨터 게임, 자율주행 등 제한적인 분야에서 주로 사용된다.
📚 지도학습 (Supervised Learning)
컴퓨터가 정답과 힌트 정보가 있는 학습 데이터를 이용해서 원하는 방향으로 데이터를 학습한다. 수학적인 모델인 머신러닝 알고리즘은 힌트와 정답 간의 관계를 계산하면서 학습한다. 여기서 힌트는 '독립변수', 정답은 '종속변수'를 의미한다.
Y = b0 + b1X
라는 모델이 있을 때, b0과 b1을 모델의 파라미터라고 한다. 학습 데이터에서 힌트와 정답 데이터 간의 관계를 가장 잘 설명하는 파라미터 값이 최적 파라미터 값이다.
✅ 분류 vs 회귀
지도학습을 적용하는 문제는 종속변수의 유형에 따라서 두 가지로 분류할 수 있다.
① 회귀 문제
• 종속변수가 연속형 변수일 때
• Linear Regression / Feed Forward Neural Network
② 분류 문제
• 종속변수가 범주형 변수일 때
• Logistic Regression / SVM / Decision Tree/ CNN, RNN
✅ Cost Function (비용함수, 손실함수) 와 경사하강법
지도학습 방식에서는 최적의 모델을 찾기 위해서 예측값과 실제값의 오차를 사용한다. IV와 DV의 관계를 가장 잘 설명한다는 것은, 반대로 설명하지 못하는 정도를 최소화한다는 의미이다. 즉, 오차를 최소화하는 파라미터를 찾는 방향으로 모델 학습이 진행된다.
학습데이터에 존재하는 전체 오차를 비용함수(=손실함수) 라고 하고, 비용함수를 최소화 하는 파라미터를 찾아야 한다. 비용함수 값이 작다는 것은 모델이 설명하지 못하는 정도가 작다는 것을 의미한다.


비용함수의 종류는 task 에 따라서(분류/회귀) 달라진다.
학습 데이터의 관측치 수 N이 많아지면, 큰 데이터의 경우 오차가 커지기 때문에 N으로 나눠서 평균치로 계산한다. MAE와 MSE 등의 지표가 대표적인데 MSE가 더 많이 사용된다. 손실함수 최적값을 찾기 위해서는 경사하강법을 통해서 미분을 해야하는데, 제곱 형태로 되어 있는 MSE가 미분이 보다 편리하기 때문이다.
📌 예시)
y: salary,
X: experience in years
Model: 𝑦 ̂= b1 * X1

위와 같은 샘플 데이터가 있을 때, 비용함수를 계산하면

해당 비용함수를 그리면 아래로 볼록한 상태가 된다.

비용함수를 최소화시키는 b1 지점을 찾아야 하는데, 여기서 b1은 미분했을 때 기울기가 0인 지점을 의미한다.

즉, 비용함수 값을 최소화시키는 지점을 찾기 위해서는 미분했을 때 기울기가 0이 나타나는 지점(=1차 도함수 값이 0이 되는)을 구하면 된다. 비용함수를 최소화시키는 값을 찾는다는 것은, 최적의 파라미터를 찾는다는 것을 의미한다.

비용함수가 아래로 볼록한 2차 함수 형태인 경우에는 정규 방정식(Normal Equation)으로 비용함수 최저 지점을 구할 수 있지만, 비용함수가 3차 이상인 경우에는 방정식으로 1차 도함수가 0이 되는 지점이 여러 곳이라서 최저점을 구할 수 없다. 따라서 머신러닝/딥러닝 에서는 경사하강법을 사용한다.
📚 경사하강법 (Gradient Descent)
✅ 경사하강법 기본 원리
• 모두 동일한 의미 : Gradient = 경사 = 접선의 기울기 = 미분값
• 하강 : 기울기를 이용해서 아래로 내려간다는 의미
경사하강법은 정규방정식처럼 비용함수 값을 최소화하는 파라미터 b1의 값을 한번에 구하는 것이 아니라, 기울기를 이용해서 bi 값을 조금씩 업데이를 진행하면서 최적값을 찾는 방법이다.
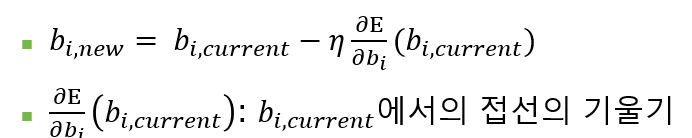
η : 학습률, 0~1사이의 값으로 한 번에 업데이트하는 정도를 정한다. 학습률이 크면 한 번에 업데이트되는 값이 큰 것이고, 작으면 한번에 업데이트 되는 값이 작다. 학습률은 사용자가 설정하는 "하이퍼 파라미터"이다.
두 번째 줄의 식은 x=bi 지점에서의 접선의 기울기를 의미한다.
경사하강법의 1 step마다 bi에서 접선의 기울기와 학습률을 곱하고, 이 값을 현재 bi에서 빼서 새로운 값을 구한다.
📌 예시
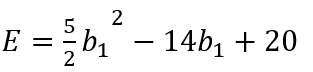
위와 같은 비용함수가 있을 때 이를 그림으로 나타내면 다음과 같다.
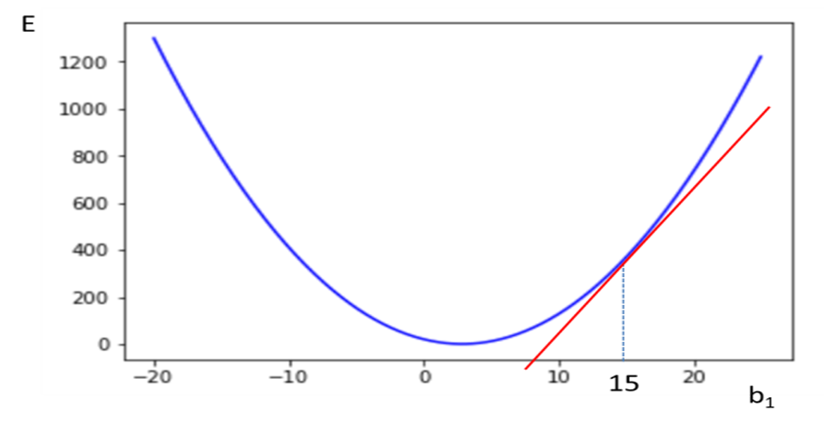
초기 시작하는 b1값은 15이고 이 값은 임의로 결정된다.

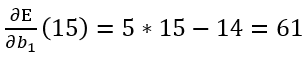
비용함수를 미분한 형태는 위와 같고, b1=15일 때의 기울기를 계산하면 61이다.

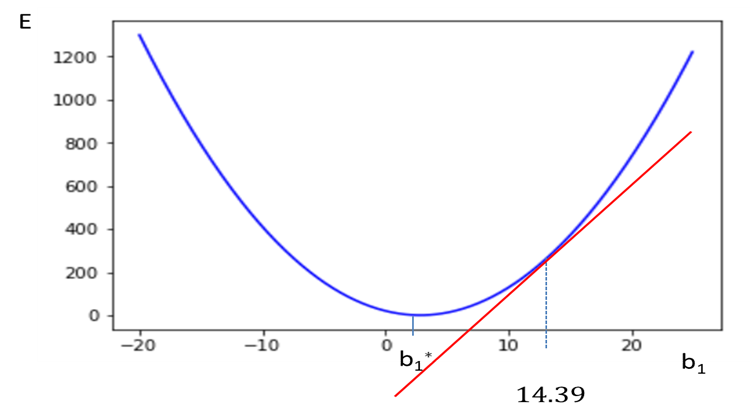
학습률=0.01 일 때, 이를 통해서 파라미터를 업데이트하면 14.39이고 위와 같이 b1이 이동한다.
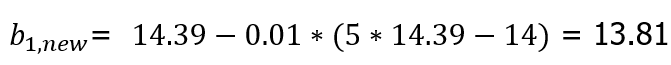
그리고 14.39에서 다시 새로운 값으로 업데이트를 진행하는 식은 위와 같다.
이 과정을 업데이트를 진행해도 b1의 값이 변하지 않을 때 까지 계속해서 반복해서 최적의 파라미터를 찾는다.
✅ 기울기 부호에 따라서 살펴보면?
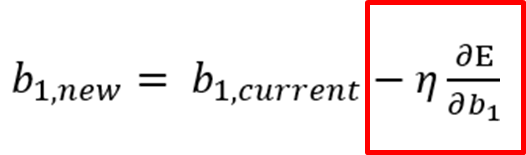
경사하강법 업데이트 식에서 빨간색인 -학습률 * 기울기 부분의 기호를 살펴보면 아래와 같다.
η > 0 인 경우)
빨간 부분의 값이 항상 양수이고, -학습률 업데이트를 진행하면서 b1이 왼쪽으로 이동한다.
η < 0 인 경우)
빨간 부분의 값이 항상 음수이고, -학습률 이 곱해지면서 양수가 되기 때문에 b1이 오른쪽으로 이동한다.

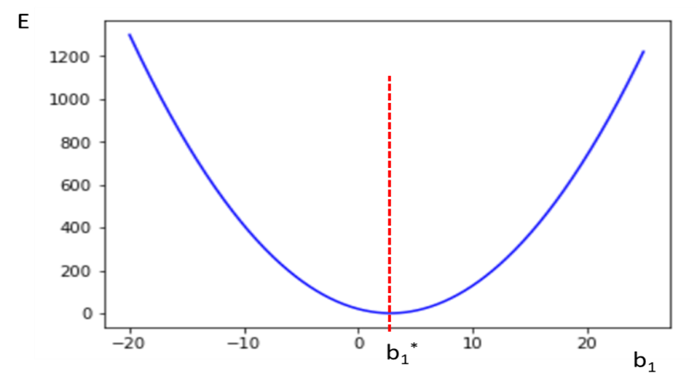
즉 부호가 어느 방향이든 항상 비용함수의 최소점으로 이동하게 된다.
📚 과적합(Overfitting)
모델이 학습 데이터에 대해서는 예측을 잘 실시하지만 새로운 데이터에 대해서는 예측 잘하지 못하는 것을 의미한다. 즉, 모델의 일반화 가능성이 떨어진다고 할 수 있음. 과적합이 발생하는 주요 원인은 다음과 같다.
(1) 모형에 포함된 파라미터나 독립변수가 너무 많아서 모형이 복잡한 경우
(2) 학습 데이터의 독립변수 값에 결과가 민감하게 반응하는 경우
이러한 과적합 문제를 해결하기 위해서는 더 많은 학습 데이터를 수집하거나, 데이터의 이상치를 제거하고 다시 학습하는 방법이 있다. 또한, 규제화 방법 또한 많이 사용된다.
✅ 규제화 (Regularization)
특정 변수에 지나치게 민감하게 반응해서 과적합이 발생하는 것을 방지하기 위해서는 해당 파라미터의 값을 작게 해야 한다. 규제화 방식은 파라미터의 크기(절댓값)를 줄이기 위해서 사용된다. 만약 파라미터의 값이 줄어서 0이 되게 되면 추가로 모델이 단순화되는 효과까지 얻을 수 있다.

규제화를 위해서는 기존 비용함수에 penalty term을 추가한다.

Lp norm을 정의하는 공식은 위와 같은데, 여기에 p=1, p=2 를 입력하면 L1 규제, L2 규제의 패널티 텀이 된다.
L1은 L1 norm 을 그대로 사용하지만 L2 norm은 계산 편의를 위해서 제곱을 실시해서 루트를 제거하고 사용한다.

위와 같은 모델이 있을 때, b는 파라미터가 모인 벡터이다.

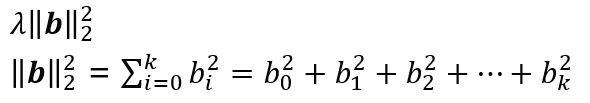
L1, L2 패널티 텀은 각각 앞에 λ를 곱해서 적용한다. λ 가 큰 경우에는 파라미터에 대한 페널티를 강하게 부여하게 된다. 만약 람다가 너무 커지게 되면 underfitting 문제가 발생할 수도 있다.
L1 방식은 파라미터를 줄여서 0까지 만들 수 있지만, L2는 0까지 만들지는 않는다. L1 방식을 사용하면 파라미터를 감소시켜서 모형을 단순화시킬 수도 있다.

L1은 절댓값이기 때문에 직선이 꺾이는 형태이고, L2는 제곱이기 때문에 2차 함수 형태이다. 위의 빨간색 식이 기존의 검은색 비용함수 식에 더해진다.
📌 예시

위에서 다룬 비용함수 예제를 다시 사용한다.

λ = 0.5이고 L2 규제화를 사용하면 위와 같이 비용함수가 구성된다.
여기서 미분을 실시해서 정규방정식으로 최적 b1값을 구해보면, b1 = 14/6 이라서 파라미터 값이 더 작아진 것을 확인할 수 있다.
(규제화 없는 비용함수 : b1 = 14/5 )

λ = 1로 할 경우에는 페널티 텀을 더 크게 반영하기 때문에 b1 = 14/7로 더 작아지는 것을 확인할 수 있다.
📚 Reference
이상엽, 연세대학교 언론홍보영상학부 부교수, 22년도 1학기 기계학습 이론과 실습
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 데이터 전처리 (2) | 2022.03.21 |
|---|---|
| [머신러닝] 선형회귀 (Linear Regression) (0) | 2022.03.14 |
| [머신러닝] 클러스터링(Clustering) (0) | 2021.12.01 |
| [머신러닝] Decision Tree (0) | 2021.10.13 |
| [머신러닝] Naive Bayes 개념 정리 (0) | 2021.10.08 |



댓글