📚 나이브 베이즈 개념
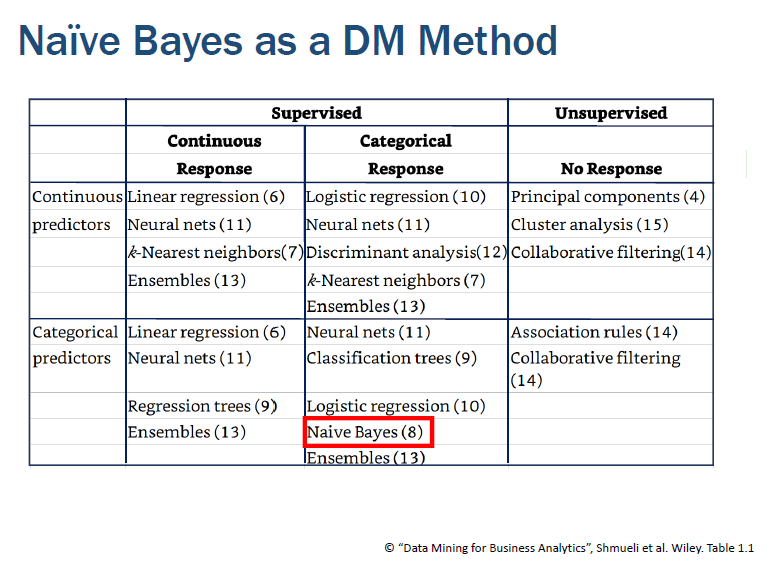
• 예측에 사용하는 특성과 결과 값 사이의 dependency relationship을 사용한다. Bayes theorem에 따라서 확률적인 계산을 수행하므로, 엄격하게 말해서 model-based 알고리즘과는 차이가 있다.
• 조건부 확률을 기반으로, 분류할 데이터가 주어졌을 때
다른 유사한 데이터 레코드들이 어떤 class로 분류되는지를 계산하는 것이 핵심 아이디어.
✅ Bayes' Theorem
· A : 알고자 하는 class(종속변수) / B : 주어진 predictor(독립변수)
· 나이브 베이즈의 핵심, Bayes' Theorem을 이용하여 P(A|B)를 계산하기 위해서 P(B|A)를 사용한다.

· 위와 같이 예측하고자 하는 레코드와 same predictor values를 공유하는 다른 레코드를 학습 데이터에서 찾아서 예측하는 것을 Exact Bayes 라고 한다. 아래의 예제는 accept 여부(종속변수)를 CC 와 online 변수(독립변수)를 이용하여 예측하는 것이다.
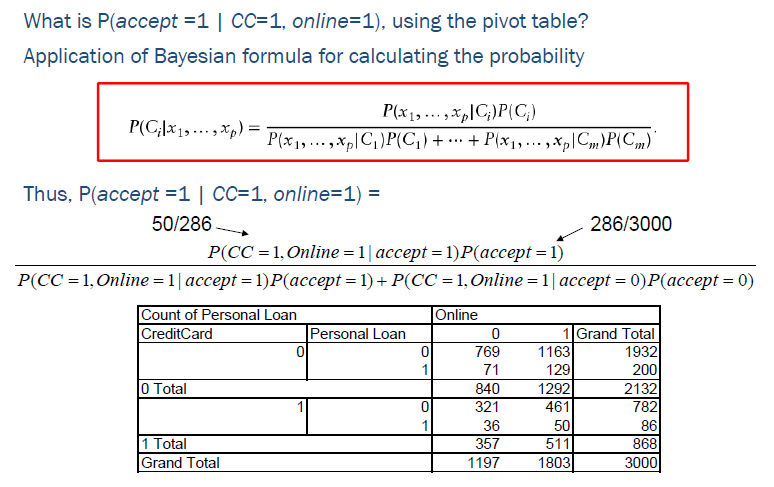
Exact Bayes는 확률 계산이기 때문에, 피벗 테이블의 형태로도 값을 구할 수 있다. 하지만, 실제 데이터에서 독립 변수가 많아지면 계산 조건과 정확하게 일치하는 레코드를 찾기가 어려워진다. 즉, 피벗 데이블에서 빈 칸이 많아져서 해당 조건을 만족하는 데이터가 존재하지 않을 가능성이 높아진다. 따라서 이를 보완하기 위해서 Naive Bayes를 사용한다.
✅ Naive Bayes

· 나이브 베이즈의 assumption은 위와 같이 독립 변수들이 서로 독립적이어야 한다는 것이다.
어느 정도 독립적이어야 하는가에 대한 정확한 기준은 없으나, 완벽하게 독립이 아니더라도 extreme dependency가 있는 것이 아니라면 robust하게 사용할 수 있다.

따라서, 앞서 작성했던 식을 위의 빨간 부분처럼 대체해서 사용할 수 있고, 훨씬 쉽게 값을 구할 수 있다.
✅ 장점
• Simple & computationally efficient
• Purely categorical 데이터에 매우 효과적이고, 데이터가 많은 경우 더 정확하다
• Independen asumption에 대해서도 꽤 robust하기 때문에 유용하게 사용할 수 있다.
✅ 단점
• 연속형 변수의 경우 범주화가 필요하다.
• 중요한 변수이지만 값이 0일 경우에는 계산식 전체의 확률이 0이 될수도 있다. 따라서 이러한 경우에는 Laplace Smoothing 기법을 사용하여, 값을 대체한다.
• 변수의 중요도나 역할에 대한 충분한 설명이 부족하다.
📚 예제 : Flight Delay 예측하기
항공편에 대한 정보와 연착 여부를 포함하고 있는 데이터로 실습을 진행하였다. 분석은 R로 진행하였다.
✅ 데이터 불러오기 및 기본 전처리
delays.df <- read.csv('FlightDelays.csv', na.strings = "")
library(e1071)
#연속형 변수를 범주형 변수로 변경
delays.df$DAY_WEEK <- factor(delays.df$DAY_WEEK)
delays.df$ORIGIN <- factor(delays.df$ORIGIN)
delays.df$DEST <- factor(delays.df$DEST)
delays.df$CARRIER <- factor(delays.df$CARRIER)
delays.df$Flight.Status <- factor(delays.df$Flight.Status)
#CRS_DEP_TIME(출발 시간) : 그룹핑(binning) 실시
summary(delays.df$CRS_DEP_TIME)
#30분 단위로 binning -> 20분을 더해서 round로 반올림
delays.df$CRS_DEP_TIME <- factor( round((delays.df$CRS_DEP_TIME + 20) / 100) )
levels(delays.df$CRS_DEP_TIME)
summary(delays.df$CRS_DEP_TIME)데이터를 로딩한 후, 나이브 베이즈 패키지인 e1071을 불러온다. 나이브 베이즈 학습 시에는 연속형 변수를 모두 범주형 변수로 변환해야 한다. CRS_DEP_TIME변수의 경우 출발 시간을 나타내는데, 범주형 변수이지만 항목이 너무 많으므로 binning을 실시한다. 시간을 30분 단위로 새로운 카테고리를 만들 수 있도록 20분을 더하여 반올림한다.
✅ Train/Test 분리 후 학습
#train/test split
train.index <- sample(c(1:dim(delays.df)[1]), dim(delays.df)[1]*0.6)
#변수 선정
train.df <- delays.df[train.index, c('DAY_WEEK','CRS_DEP_TIME','ORIGIN','DEST','CARRIER','Flight.Status')]
valid.df <- delays.df[-train.index, c('DAY_WEEK','CRS_DEP_TIME','ORIGIN','DEST','CARRIER','Flight.Status')]
#나이브베이즈 학습
delays.nb <- naiveBayes(Flight.Status~., data=delays.df)
delays.nb학습 및 테스트 데이터를 분리하고, 학습에 사용할 변수를 선정한다. 여기서는 별도의 feature selection 과정을 거치지 않고 분석자가 임의로 유의미할 것이라고 판단한 변수를 사용하였다. 그리고 naiveBayes() 함수를 이용하여 학습을 실시한다.
✅ 예측값 확인
#valid 행마다 확률값 계산
pred.prob <- predict(delays.nb, newdata = valid.df, type = 'raw') #type 값 지정하면 확률 다 보여줌
pred.prob
#valid 행마다 최종 분류 결과 계산
pred.class <- predict(delays.nb, newdata = valid.df) #cutoff 0.5 기준
pred.class
#데이터프레임으로 만들기
df <- data.frame(actual = valid.df$Flight.Status, prdicted = pred.class, pred.prob)
#특정 조건을 만족하는 값의 예측 결과 출력
df[valid.df$CARRIER == "DL" & valid.df$DAY_WEEK == 7 & valid.df$CRS_DEP_TIME == 10,]predict() 를 이용하여 valid 데이터에 대해서 예측 값을 계산한다. type='raw'를 포함하면 probability를 보여주고, 없을 경우 최종 class만 보여준다.
✅ 성과 평가 : ROC Curve / Lift Chart
###ROC
library(pROC)
ROC_flight <- roc((ifelse(valid.df$Flight.Status == 'delayed', 1,0)), pred.prob[,1]) #delayed, ontime이 문자로 되어있으므로, 숫자로 변환
plot(ROC_flight, col = 'blue')
auc(ROC_flight)
###Lift Chart
library(gains)
gain <- gains(ifelse(valid.df$Flight.Status == 'delayed', 1,0), pred.prob[,1], groups = 10)
gain
plot(c(0, gain$cume.pct.of.total*sum(valid.df$Flight.Status == "delayed")) ~ c(0, gain$cume.obs),
xlab="# cases",
ylab="Cumulative",
main="",
type="l")
lines(c(0,sum(valid.df$Flight.Status == "delayed"))~c(0, dim(valid.df)[1]), lty=2)

모델에 대해서 ROC 커브와 Lift Chart를 시각화하면 위와 같다.
✅ 성과평가 : Confusion Matrix
### confusion matrix 만들기
library(caret)
#train 데이터
pred.class <- predict(delays.nb, newdata = train.df)
pred.class
confusionMatrix(pred.class, train.df$Flight.Status)
#valid 데이터
pred.class <- predict(delays.nb, newdata = valid.df)
confusionMatrix(pred.class, valid.df$Flight.Status)
#cutoff 값을 바꿔서 Recall 높이기
pred.probth <- factor(ifelse(pred.prob[,2] >= 0.3, 'delyaed','ontime'))
class(pred.probth)
#levels(valid.df$Flight.Status) <- levels(pred.probth)
confusionMatrix(pred.probth, valid.df$Flight.Status)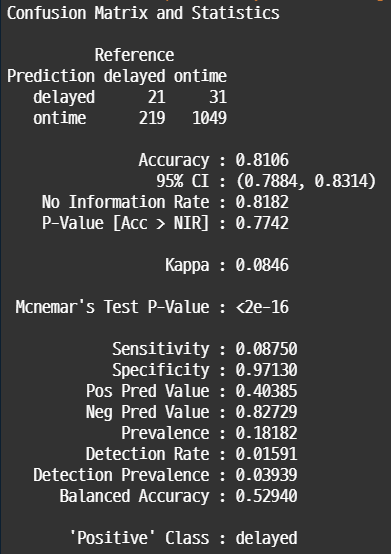
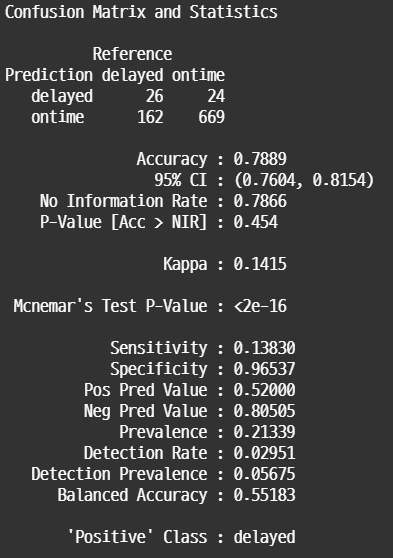

Train data, Valid data, Cutoff 조정 후 데이터에 대해서 Confusion Matrix를 살펴보면 위와 같다. 당연한 결과이지만 train data보다 valid data의 전체 정확도가 감소했다. Sensitivity가 상당히 낮게 나타나는데, 이를 보완하기 위해서 cutoff 값을 0.3으로 낮게 조정하였다. 그 결과 recall이 0.5로 향상된 것을 확인할 수 있다.
📚 자료 출처
• Data Mining for Business Analytics: Concepts, Techniques, and Application in R" by R, Galit Shmueli, Peter C. Bruce, Inbal Yahav, Nitin R. Patel, Kenneth C. Lichtendahl Jr. Wiley. 1st edition. Wiley, 2017.
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 선형회귀 (Linear Regression) (0) | 2022.03.14 |
|---|---|
| [머신러닝] 지도학습 / 경사하강법 / 규제화 (0) | 2022.03.07 |
| [머신러닝] 클러스터링(Clustering) (0) | 2021.12.01 |
| [머신러닝] Decision Tree (0) | 2021.10.13 |
| [머신러닝] KNN 개념 정리 (0) | 2021.10.06 |




댓글