📚 군집화
각 문서에 대한 label 정보가 필요 없는 대표적인 unsupervised learning 방식이 군집화이다.
데이터포인트간의 유사도를 기반으로 유사한 데이터포인트끼리 묶어서 그룹을 생성한다.

군집화는 각 데이터 샘플(=관측치=row)의 정보를 하나의 종 벡터로 간주하고 계산한다.
이 과정에서 사용되는 변수(=벡터)는 내가 수행하고자 하는 task에 적합한 것이어야 한다.
여기서는 K-means, 계층적 군집화, DBSCAN 에 대해서 정리한다.
📚 K-Means
가장 대표적인 알고리즘으로, 유클리디안 거리(Euclidean distance)를 사용해서 벡터(데이터 포인트)간의 거리를 계산하고 그룹화한다.
✅ 계산 방식
k-means 알고리즘은 군집의 수 k를 분석자가 설정해야 한다.
k=3 이라고 했을 때,

임의로 k 개의 점을 선택하고 이를 각 군집의 중심이라고 가정한다.

중심이 아닌 점(흰색) 각각에 대해서 각 중심점과의 거리를 계산해서 가까운 점이 속한 그룹으로 할당한다.

해당 군집에 속한 벡터의 평균값을 이용해서 군집별로 새로운 중심으로 업데이트한다(세모 점).
여기서 세모 점들은 실제 데이터에는 없는 가상의 포인트이다.

각 데이터 포인트와 새롭게 업데이트된 중심점에 대해서 유클리디안 거리를 계산하고 그룹을 다시 할당한다.
이 과정을 더이상 군집에 변경이 발생하지 않을 때 까지 반복하거나, 분석자가 원하는 횟수만큼 반복한다.
✅ 실루엣 계수 (Shilhouette score)

같은 군집에 있는 관측치들이 얼마나 가깝고 다른 군집에 있는 관측치들이 얼마나 먼 지를 나타내는 지표.
각 클러스터에 대해서 -1~1의 값을 가지는데, 1에 가까울수록 군집화가 잘 되었다고 볼 수 있다. 각 클러스터의 실루엣 계수가 대부분 높은 값을 가지고 있다면 전체 데이터에 대해서 전반적으로 군집화가 잘 되었다고 볼 수 있다.
만약 일부 군집에서 너무 낮거나 음수인 값이 나타난다면 다른 방식으로 군집화를 시도해봐야 한다.
실루엣 스코어는 완벽하고 절대적인 지표는 아니다. 해당 task의 목적과 도메인 지식을 바탕으로 하되 실루엣 스코어는 참고용으로 사용하는 것이 적절하다.
📚 계층적 군집분석 (Hierarchical Clustering)
계층적 군집화는 두 가지 방식이 있다. (Agglomerative vs Divisive) 주로 사용되는 방식은 agglomerative(응집하는) 방식이다.
✅ Agglomerative 방식
이름 그대로 개별 데이터 포인트를 연결하는 것 부터 시작해서 최종적으로 하나의 커다란 군집으로 합쳐(응집)지는 방식이다.
bottom-up approach에 해당한다.
반대로 Divisive 방식은 모든 데이터 포인트 전체를 하나의 군집으로 보고, 연결을 끊어가는 방식으로 진행한다.
Top-down 방식이고 Agglomerative에 비해서 적게 사용된다.
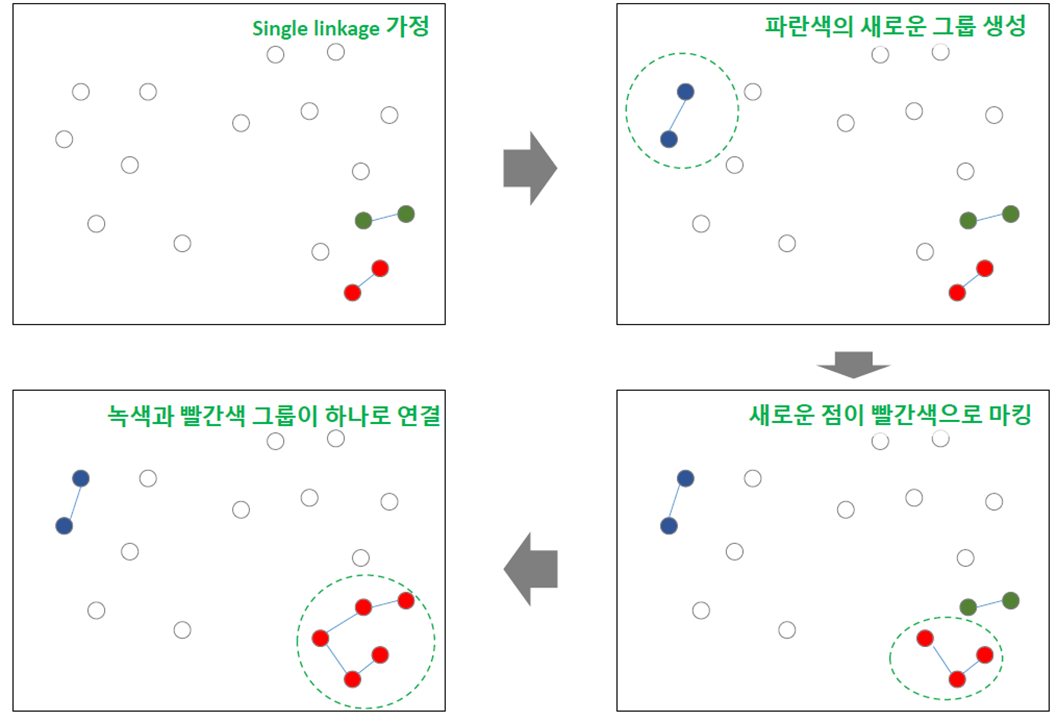
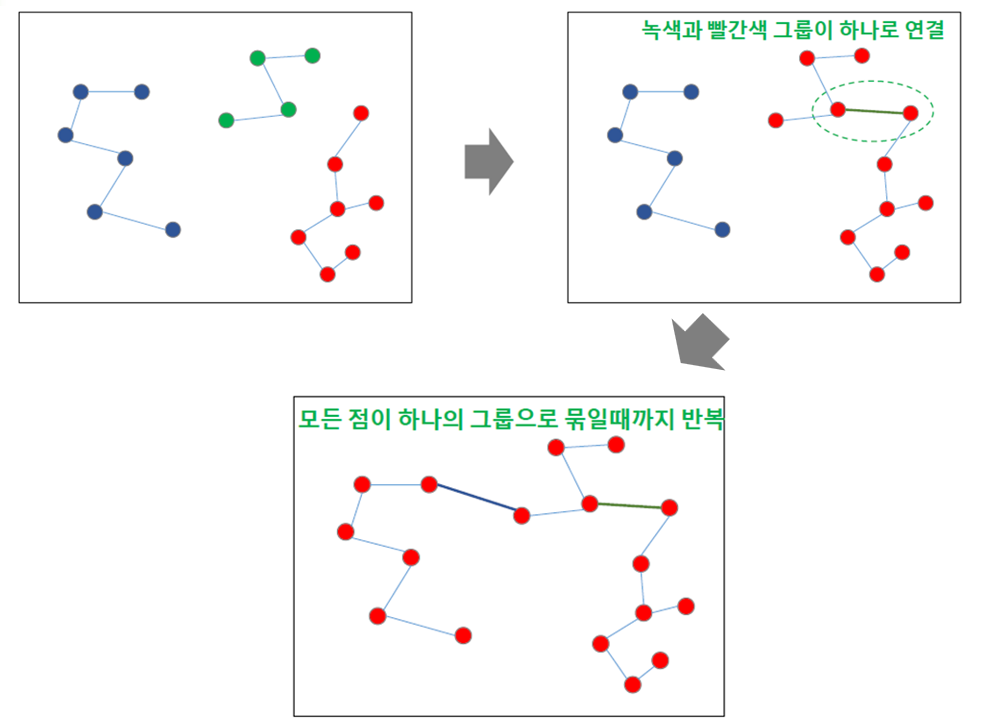
각 데이터 포인트를 개별 클러스터로 간주하고 시작한다(클러스터 1개=데이터 포인트 1개). 거리가 가까운 군집들을 순차적으로 연결해서 최종적으로 모든 군집들이 연결되어서 하나가 될 때 까지 진행한다.
📌Dendrogram
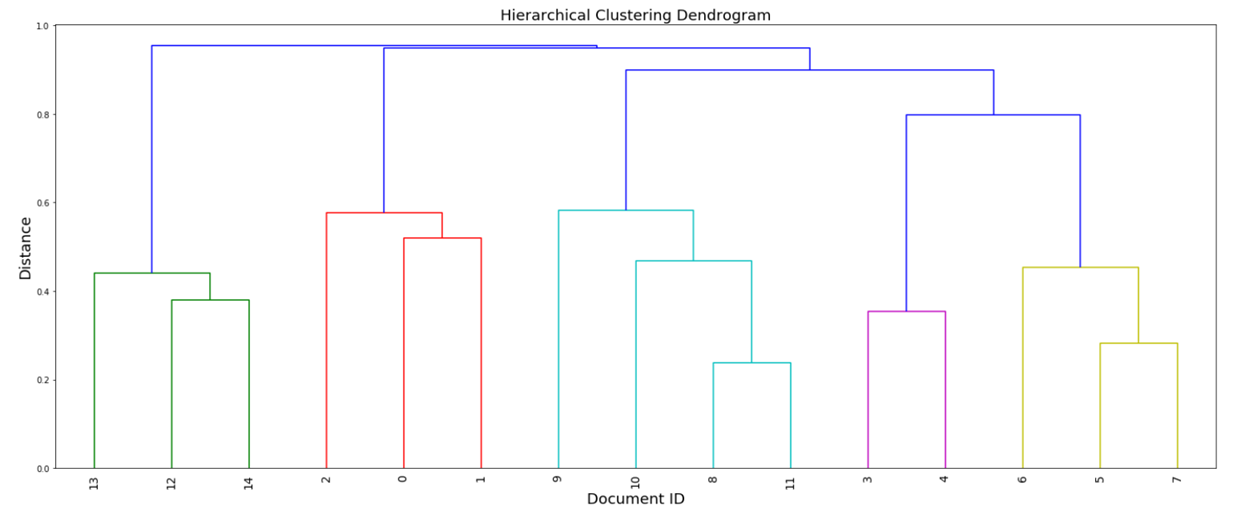
• 가로 : 관측치
• 세로 : 군집 간의 거리
위와 같이 agglomerative 군집화를 단계별로 시각화하면 dendrogram으로 나타낼 수 있다.
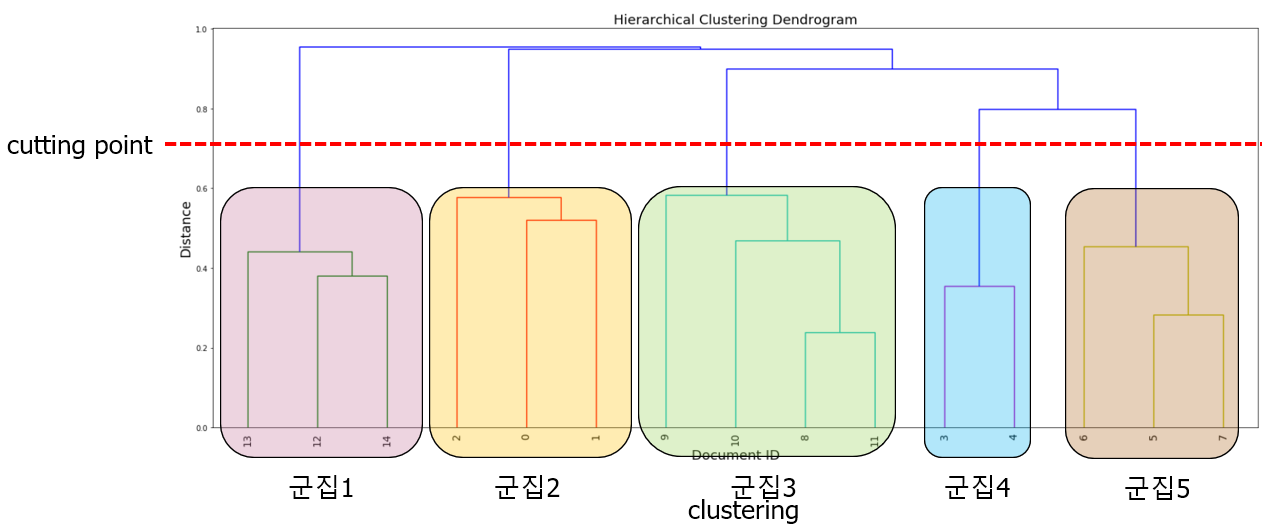
K-means와 마찬가지로 군집의 수를 정해야 하는데, 분석가의 판단에 따라서 cutting point를 설정한다. 위 그림의 경우 군집이 5개가 된다.
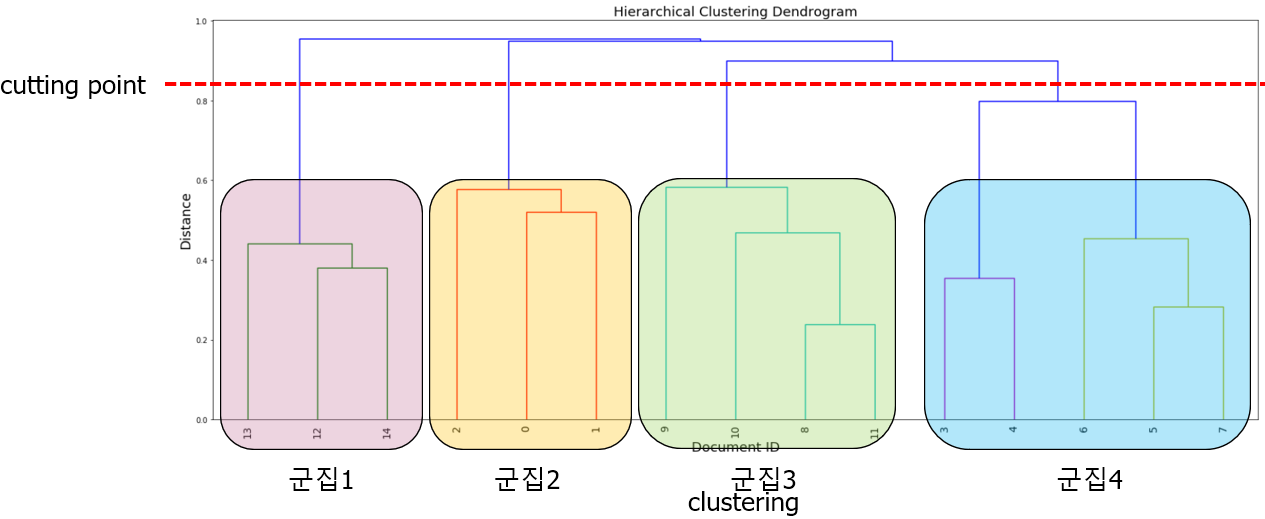
dendrogram을 사용할 경우에는 시각적으로 적절한 군집의 수를 확인할 수 있다.
위의 같이 군집수=4(빨간 점선)로 설정했을 경우에는 군집 4의 하위에 속하는 데이터 포인드들 간의 거리가 어느정도 있다는 것을 확인할 수 있다. 따라서, 군집 4를 한번 더 나눠서 군집수=5로 설정하는 것이 낫다는 것을 시각적으로 확인할 수 있다.
(하지만 이것도 상대적인 기준이며 절대적인 것은 아니다)
📌 클러스터 간 거리 계산 방식
계층적 군집화에서는 유클리디안 거리, 코사인 유사도 모두 사용 가능하다.
각 클러스터 내부의 데이터 포인트가 1개라면 간단하게 유사도를 계산할 수 있지만, 각 군집 내에 데이터 포인트가 여러개 존재할 경우 거리 계산이 난감해진다. 이러한 경우 거리를 계산하는 방식은 여러개가 있다.
1) Single
각 군집의 데이터 포인트 중에서 가장 가까운 데이터 포인트간의 거리를 사용함
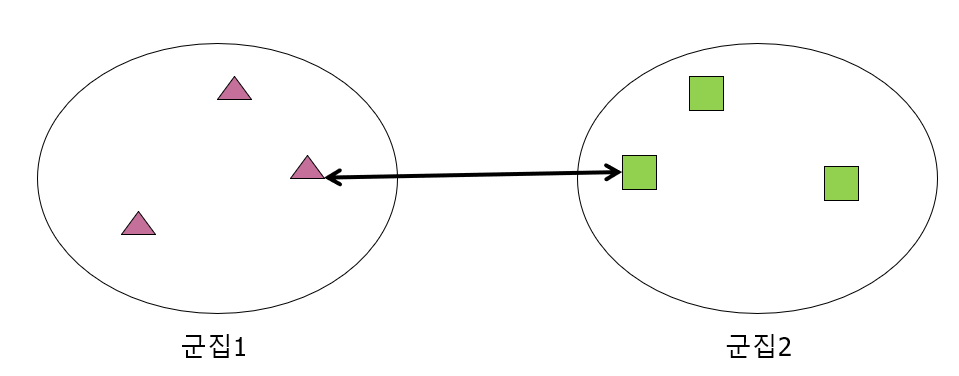
2) Complete
각 클러스터를 구성하는 데이터 포인트 중에서 가장 먼 데이터 포인트 간의 거리를 사용
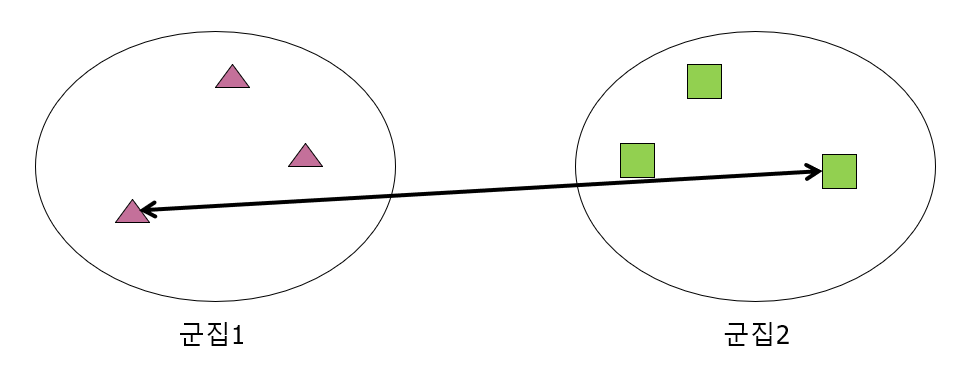
3) Average
각 클러스터를 구성하는 데이터 포인트들 간의 평균 거리

4) Ward
1~3번 방식처럼 거리가 아닌 데이터 포인트의 분산을 기반으로 계산한다.
두 개의 클러스터를 합쳤을 때 데이터 포인트들이 갖는 분산이 가장 작은 클러스터 끼리 묶어주는 방법.
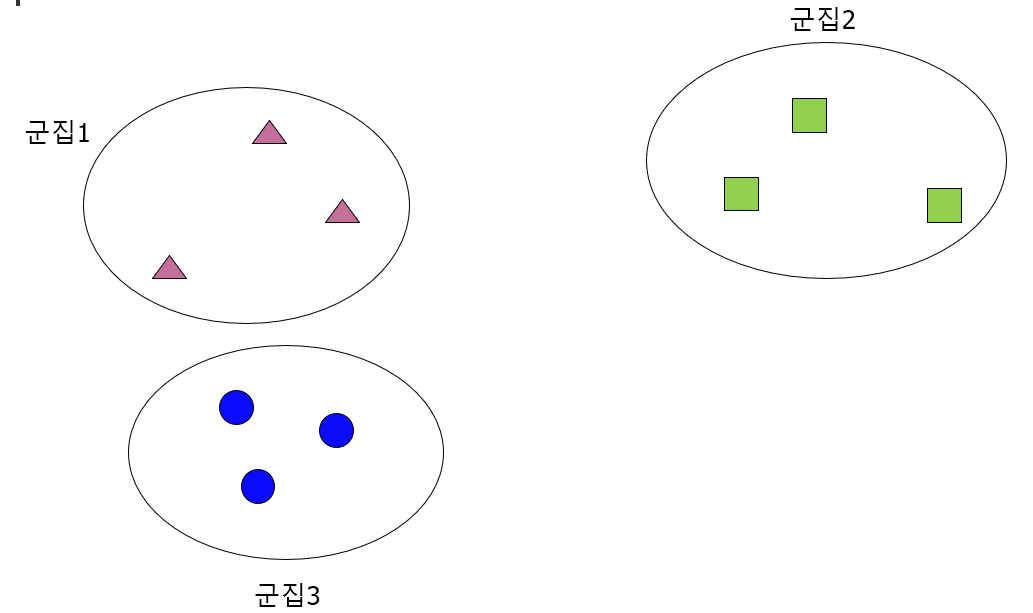
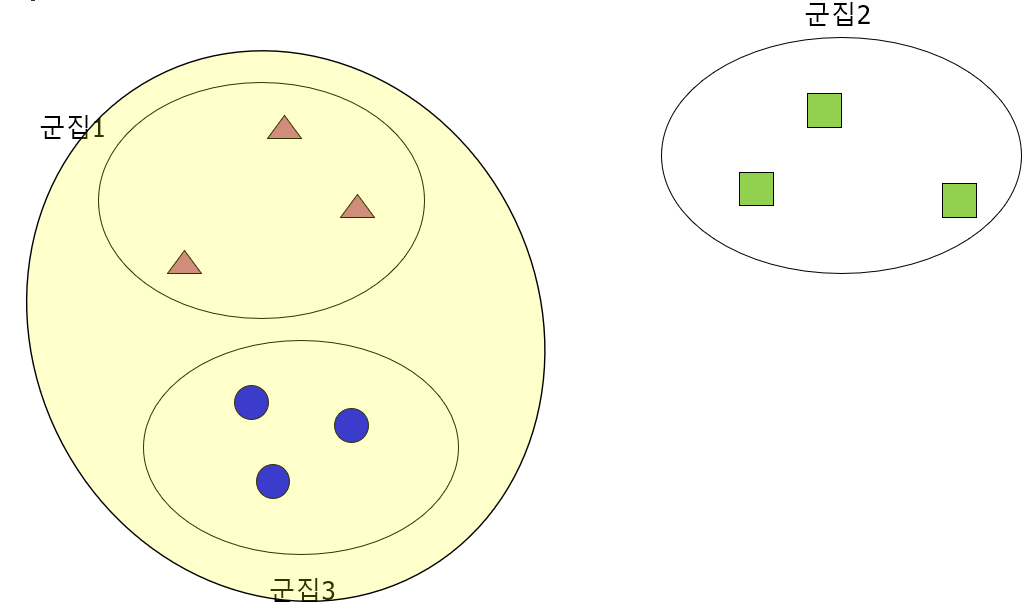
위와 같이 군집이 분포가 되어 있을 때,
[군집1+군집2] 보다 [군집1+군집3] 을 묶는 것이 분산이 적게 나타나기 때문에 1,3을 먼저 묶는다.
📌 적절한 거리 계산 지표 선택방법
http://scikit-learn.org/stable/modules/clustering.html#hierarchical-clustering
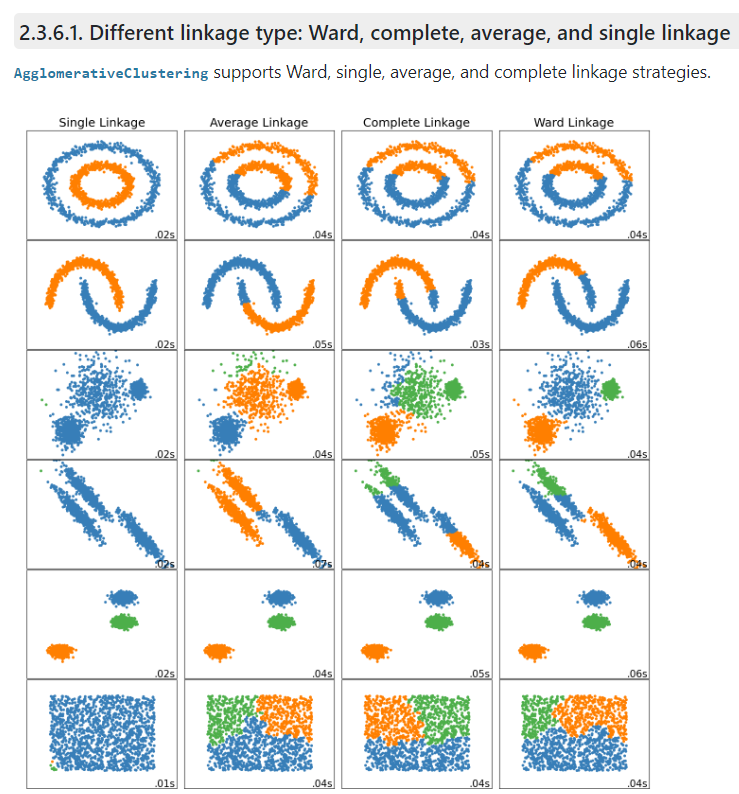
적절한 거리 계산 방식을 선택하기 위해서는 데이터를 2차원으로 먼저 시각화 해보는 것이 도움이 될 수 있다. 시각화를 통해서 데이터 분포를 확인하고 일반적으로 성능이 좋다고 알려진 방식을 선택할 수 있다.
📚 DBSCAN
DBSCAM : Density-Based Spatial Clustering of Applications with Noise
데이터가 밀집된 정도를 가지고 서로다른 군집을 구분한다. 즉, 서로 밀집된 데이터 포인트들을 하나의 군집으로 분류한다.
앞선 군집화 기법들과는 달리 분석가가 군집의 개수를 설정하지 않아도 되는 non-parametric algorithm에 해당한다. 또한, DBSCAN에서는 어떠한 군집으로도 분류되지 않는 아웃라이어가 존재한다.
📌 용어
ε : 특정 데이터 포인트의 반경을 의미함.
이를 이용해서 하나의 데이터 포인트에서 다른 데이터 포인트로 연결할 지 여부를 결정한다.
ε 안에 다른 데이터 포인트가 있으면 연결하고 그렇지 않으면 연결 X
✅작동 방식 : 데이터 포인트의 유형

ε = 1, MinPts=3 (자기자신 포함)
1) 코어 포인트(core point)
특정 데이터 포인트 p에 대해서 반경 ε 안에 특정 수 이상(minPts)의 데이터 포인트가 존재하는 경우
코어 포인트만이 다른 데이터 포인트로 연결할 수 있다. (다른 데이터 포인트는 다른 포인트로 연결이 불가능함)
2) 직접 도달 가능한 포인트(directly reachable point)
만약 데이터 포인트 q가 core point p로 부터 ε 거리 안에 존재한다면 q는 p로 부터 직접적으로 도달 가능한 포인트라고 부른다.
3) 도달 가능한 포인트(reachable point)
만약 데이터 포인트 q가 코어 데이터 포인트 p로부터 직접 도달 가능한 (directly reachable) 포인트는 아니지만,
중간에 위치하는 다른 데이터 포인트들을 통해서 (간접적으로) 도달 가능한 경우.
위 그림에서 q1은
p3를 기준으로 하면 직접 도달 가능한 포인트이고
p1, p2를 기준으로하면 도달 가능한 포인트이다.
4) 이상치 (outliers)
다른 어떠한 데이터 포인트로부터도 도달 불가능한 데이터 포인트를 의미한다.
위의 방식으로 각 데이터를 분류하면서 코어 포인트를 중심으로 군집을 연결한다.
🏷️K-means / 위계적 군집화와의 차이점
1. DBSCAN은 군집의 수를 분석자가 설정하지 않는다. 알고리즘에 따라서 자동으로 군집의 수가 결정된다.
2. 특정한 군집에 속하지 않는 아웃라이어가 존재한다.
DBSCAN은 사용되는 횟수는 상대적으로 적지만, task와 도메인에 따라서 성능이 좋게 나타날 수도 있다.
📚 Reference
이상엽, 연세대학교 언론홍보영상학부 부교수, 22-1학기 기계학습 이론과 실습
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| [머신러닝] Confusion Matrix, ROC Curve (0) | 2022.04.11 |
|---|---|
| [머신러닝] Logistic Regression (0) | 2022.04.11 |
| [머신러닝] 데이터 전처리 (2) | 2022.03.21 |
| [머신러닝] 선형회귀 (Linear Regression) (0) | 2022.03.14 |
| [머신러닝] 지도학습 / 경사하강법 / 규제화 (0) | 2022.03.07 |


댓글