📚 GMM
✅ 개요
• KNN, 위계적 군집화, DBSCAN 등의 알고리즘은 벡터간 유사도로 군집화를 실시한다. 반면 GMM은 관측된 데이터가 특정 확률 분포를 이용해서 생성되었다고 가정하는 확률 모델이다.
• GMM은 독립변수에 대한 다변량 분포(multivariate distribution)를 사용해서 데이터가 생성되었다고 가정한다. 하나의 분포가 하나의 군집을 의미하고, 다변량 분포에서는 여러 개의 확률 분포(=여러 개의 피쳐)를 사용한다. GMM에서는 각 분포가 가우시안 분포(=정규 분포)를 따른다.
✅ 정규 분포 (= 가우시안 분포)
독립변수가 하나인 경우 정규분포는 아래와 pdf를 따른다.

정규분포의 주요 파라미터는 평균과 분산이고 아래와 같이 표현할 수 있다.

독립변수가 1개인 데이터가 있을 때 아래와 같이 직선 위에 나타낼 수 있다
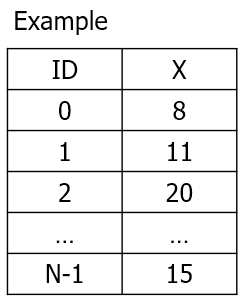

관측치를 직선위에 나타내보면 간격이 다르게 나타나는데 이 분포는 정규분포를 따른다. 그리고 하나의 정규분포가 아니라 여러개의 정규분포를 통해서 나타낸다. 위의 경우에는 각각의 군집을 3개의 정규 분포로 생성했다고 가정할 수 있다.

각각의 분포는 평균과 분산이 모두 다르다. 평균과 분산은 파라미터이므로, GMM에서 학습을 진행하면 최적의 평균과 분산을 계산하게 된다. 위의 경우는 독립변수가 1개인 경우이지만 실제 데이터는 변수가 2개 이상이다. 여러 개의 독립변수에 대한 분포를 '다변량 정규분포' 라고 부른다.
✔ 정규분포의 분산의 의미 :
위 그림에서는 초록색 분포가 분산이 작다. 따라서 해당 분포를 이용해서 생성된 관측치가 상대적으로 촘촘하게 모여있다고 볼 수 있다.
✅ Mixture Model (혼합 모형)
• 혼합 모형 : 데이터가 하나의 확률 분포가 아니라 여러개의 확률 분포를 이용해서 생성되었다고 가정한 모형.
데이터가 서로 다른 두 개의 정규 분포를 이용해서 생성되었다고 가정하면, 데이터 중에서 한 관측치 xi의 확률은 아래와 같이 표현할 수 있고 이러한 식으로 표현할 수 있는 모델을 확률 모형이라고 한다. 여기서 평균, 분산, π가 핵심 파라미터가 된다.

xi가 두 개의 분포 중에서 어떤것을 사용하였는지를 반영하기 위해서 확률을 나타내는 π를 사용한다.
πi,1 는 특정 관측치가 첫 번째 분포를 이용해서 생성된 경우이고 πi,2는 특정 관측치가 두 번째 분포를 이용해서 생성된 확률을 의미한다. 이 두개의 관측치를 mixing coefficient 또는 weight라고 한다. 만약 3개의 분포를 이용해서 관측치가 생성된다고 하면 πi, 3 에 대한 식이 추가된다.
mixing coefficient를 나타내기 위해서는 z 라는 잠재변수를 사용한다.
• z = i 번째 관측치가 생성될 때 사용된 분포를 나타내는 변수
즉, z1은 i 번째 관측치가 첫 번째 정규분포를 이용해서 생성되었다는 것을 의미하고, z2는 i번째 관측치가 두 번째 정규분포를 이용해서 생성되었다는 것을 의미한다.
따라서 P(zi=1)는 xi가 첫 번째 정규분포를 이용해서 생성될 확률을 의미한다.
P(zi=2)는 xi가 두 번째 정규분포를 이용해서 생성될 확률을 의미한다.

독립변수의 수가 M개 라고 하면 다변량 정규 분포는 아래와 같이 표현할 수 있다.

공분산 행렬은 PCA 부분 참고. 여기서는 변수가 M개이므로 공분산 행렬은 MxM 형태이다.

✅ 독립변수의 수가 2개인 경우 (이변량 정규분포)
피쳐의 수가 2개이면 2차원 공간에 표현이 가능하다.
서로 다른 여러개의 이변량 정규 분포(독립변수가 2개라서)를 사용해서 데이터가 생성되었다고 가정한다.
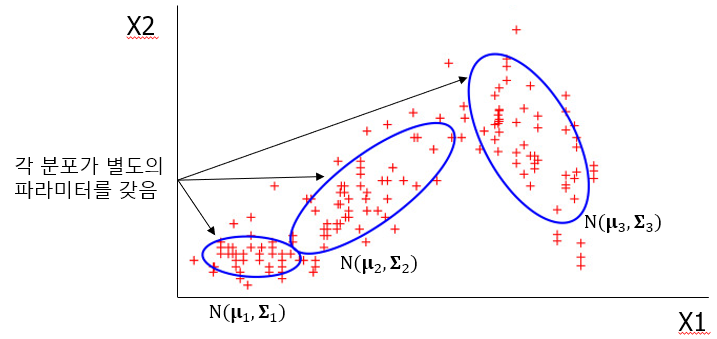

앞서서 변수가 1개인 경우와 다르게 여기서는 변수가 2개이기 때문에, 각 분포의 평균은 두 개 변수의 평균으로 구성된다.
위 상태에서 GMM를 사용해서 계산해야 하는 것은 아래와 같다.
• 데이터를 생성하는데 사용된 각 정규 분포의 파라미터 : 평균과 분산
• 각 관측치가 각 분포에 속할 확률 (mixing coefficients) : π
위 상황에서 특정 관측치 xi의 확률은 아래와 같이 표현할 수 있다. 이 때 각 관측치의 확률은 확률 모형의 파라미터(평균, 분산, 파이) 값에 따라서 달라진다. 특히 π 가 가장 어떤 확률 분포를 따를지를 결정하는 역할을 하기 때문에 중요하다.

📌 GMM에서 최대우도추정(MLE)의 사용
GMM에서는 주요 파라미터인 평균, 분산, π를 사용하기 위해서는 최대우도추정(Maximum Likelihood Estimation)을 사용한다. GMM은 로지스틱 회귀와 동일하게 확률 모형이기 때문에 이 방식을 사용할 수 있다.
MLE는 likelihood를 최대화 하는 파라미터를 찾는 방법이다. likelihood는 우리가 가지고 있는 데이터의 확률을 의미한다.
N개의 관측치가 있는 데이터 X에 대해서,
likelihood를 아래와 같이 조건부 확률 형태로 나타낼 수 있다.
likelihood를 계산할 때에는 독립변수가 서로 독립이라고 가정하기 때문에 Π 를 이용해서 수열의 곱셈으로 나타낼 수 있다.

그러나 곱셈이 있으면 미분이 힘들기 때문에 로그를 붙여서 log-likelihood를 사용한다. 로그를 붙이고 위에서 xi 의 확률을 나타내는 식을 이용하여 식을 정리하면 아래와 같다.
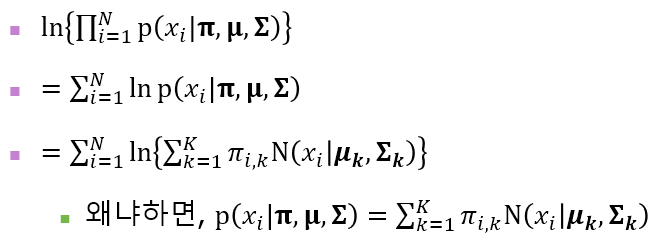
가장 마지막 식으로 나타내면 결국 likelihood를 파라미터(평균, 분산, π)에 대한 함수로 나타낼 수 있고, log-likelihood는 위로 볼록한 함수 형태이기 때문에 미분을 해서 미분값이 0인 방정식을 푸는 정규방정식 방법을 사용하면 maximization 문제를 쉽게 풀 수 있다. → MLE
* 참고로 optimization 방식에는 1.정규방정식 2. 경사하강법 이 있다)
하지만 여기서는 π 파라미터 때문에 정규방정식 방식을 직접적으로 사용할 수 없다. π 는 z라는 잠재변수(눈에 보이지 않는 변수)가 특정한 값을 가질 확률을 의미한다.

따라서 이 값을 직접 구할 수가 없기 때문에 정규방정식으로 파라미터 값을 한번에 구할수가 없다. 따라서 EM 알고리즘을 대신해서 사용한다.
📌 EM(Expectation Maximization) 방법
혼합모형에서 모형의 파라미터를 찾기 위해서 사용하는 방법. log likelihood를 최대화 할 때 아래 값을 먼저 계산해야 한다.

하지만 | 뒤 부분의 값을 실제로 계산을 할 수가 없기 때문에,
이 값들을 임의의 값에서 시작해서 zi를 업데이트하면서 log likelihood를 최대화하는 파라미터를 찾는다.
이 과정을 파라미터가 특정 값으로 수렴할 때 까지 반복하면, 최종적으로 수렴하는 π를 찾을 수 있다.
π를 알면 특정 관측치 xi가 어떤 분포에 속하는지 알 수 있기 때문에 군집을 할당할 수 있다.
📚 예시
임의의 데이터셋을 생성해서 GMM으로 군집화를 하고, AIC와 BIC로 성능을 평가한다.
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
#데이터 생성
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:,0], X[:,1])
이 경우에는 관측치가 2차원 상에 나타나기 때문에 사용한 독립변수(=분포 수)가 2개인 경우이다.
gmm = GaussianMixture(n_components=4)
gmm.fit(X)log likelihood 함수를 최대화하는 파라미터를 계산한다. 군집 수는 4개로 정한다.
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
#관측치 라벨 확인
labels
#파이 값 확인
gmm.predict_proba(X)
labels를 통해서 관측치의 군집을 알 수 있다. 또한 predict_proba를 통해서 π 값을 확인할 수 있다. 여기서는 군집 수를 4개로 설정했기 때문에 관측치마다 π 값이 4개가 출력된다.
✅ AIC 와 BIC
K means의 경우 최적의 k 확인 및 군집 성능 평가를 위해서 실루엣 계수를 사용했다. GMM은 확률 모델이기 때문에 실루엣 계수가 아닌 log-likelihood 기반인 AIC(Akaike Iinformation Criterion)와 BIC(Bayesian Information Criterion)를 사용한다.

• s : 파라미터의 수
• N : 관측치의 수
likelihood는 확률값이므로 0~1 사이의 값을 가지며, 모델이 데이터를 잘 설명할수록 값이 커진다.
likelihood가 0~1사이이므로 log-likelihood는 음수가 되고, 모델의 성능이 좋을수록(=likelihood가 클수록) 커진다. 즉, 절대값은 작아진다.
AIC와 BIC는 모두 log likelihood는 앞에 -2가 붙어있기 때문에 모델의 성능이 좋을수록 값이 작아진다. 따라서 GMM은 AIC 또는 BIC가 최소화되는 것을 기준으로 군집 갯수를 선정한다.
n_components = np.arange(1, 21)
models = [GaussianMixture(n, covariance_type='full', random_state=0).fit(X) for n in n_components]
plt.plot(n_components, [m.bic(X) for m in models], label='BIC')
plt.plot(n_components, [m.aic(X) for m in models], label='AIC')
plt.legend(loc='best')
plt.xlabel('n_components');
여기서는 군집의 개수가 4일때 AIC와 BIC가 가장 적게 나타난다.
📚 Reference
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| 서포트 벡터 머신 (Support Vector Machine) (0) | 2022.06.18 |
|---|---|
| 특이값 분해 (Singular Value Decomposition) (0) | 2022.06.17 |
| 차원축소 - PCA(Principal Component Analysis) (0) | 2022.05.30 |
| 차원축소 기본 - 고유값, 고유벡터, 고유분해 (0) | 2022.05.29 |
| 앙상블 기법(Ensemble Method) - Boosting (0) | 2022.05.28 |




댓글