📚Boosting
- Adaboosting, Gradient Boosting

Boosting 방식은 sub sample을 사용하지 않고 원래의 학습 데이터에 여러 개의 weak learner를 순차적으로 적용한다. 이전 learner가 잘못 예측한 부분을 이후의 learner가 보완하는 방식으로 학습이 진행된다. Gradient boosting, Adaptive boosting이 여기에 속한다. 최근에는 배깅보다 부스팅 방식이 성능이 더 뛰아나서 많이 사용된다.
부스팅 방식에서는 각 data point에 유니크한 가중치가 부여되는데, 이전 learner에서 제대로 예측하지 못한 data point의 경우 다음 learner에서 가중치를 더 크게 부여해서 올바르게 학습되도록 유도한다.
📚 AdaBoosting (Adaptive Boosting)
Freund, Y., Schapire, R., & Abe, N. (1999). A short introduction to boosting. Journal-Japanese Society For Artificial Intelligence, 14(771-780), 1612.
에이다 부스트는 기본적인 부스팅 방식으로 이전 학습기에서 제대로 예측하지 못한 data point를 다음 단계에서 더 많이 고려하도록 학습한다. 에이다 부스트에서 종속변수가 취할 수 있는 값은 +1과 -1이다. 작동 순서는 다음과 같다.
① 학습 데이터에 모든 관측치의 가중치를 동일하게 1/n로 설정한다. 가중치의 합은 1이다. 각 weak learner에 대해서 아래 과정을 반복한다.
② 각 관측치의 가중치에 따라서 sub sample 을 추출한다. 가중치가 높을수록 sub sample에 뽑힐 확률이 높아진다. 첫 단계에서는 각 관측치가 sub sample에 포함될 확률이 동일하다.
③ 각 sub sample에 대해서 학습을 진행하고 학습 결과를 원본 데이터에 적용해서 Total Error(TE)를 계산한다. 에러는 "잘못 분류된 관측치 / 전체 관측치" 로 계산한다.
④ 아래와 같이 전체 모형의 성능을 계산한다. 여기서 TE는 전체 에러, t는 weak learner의 단계를 의미한다.

⑤ t 단계에서의 가중치를 아래와 같이 업데이트 한다.

예를 들어 전체 데이터가 10개이고, t=2 일때의 가중치를 계산한다. 첫 번째 단계에서는 가중치가 동일하므로 wt-1 = 1/10 이고, ⍺t-1=1 이라고 가정한다. 이를 바탕으로 가중치를 업데이트 하면 아래와 같다.
• 잘못 분류된 관측치 : w2= (1/10) * e1
• 올바르게 분류된 관측치 : w2 = (1/10) * e-1
⍺t > 0인 경우에는 위의 업데이트 식에 따라서 잘못 분류된 관측치의 가중치가 커지고, 올바르게 분류된 경우에는 가중치가 작아진다. 따라서 잘못 분류된 샘플들은 다음 단계에서 sub sample에 포함될 확률이 높아진다.
가중치를 업데이트하고 나서 다시 ② 부터 순서대로 진행한다.
⑥ 새로운 관측치에 대해서 종속변수를 예측할 때에는 아래 식을 이용한다. 여기서 Mt(x)는 각 단계의 weak learner가 예측한 값을 의미한다.
⍺t 는 ④에서 사용한 각 단계별 learner의 성능을 나타낸다. 따라서 아래 식에 따르면 각 단계별 learner의 성능에 따라서 예측값에 대해서 가중치를 부여한다. (성능이 좋은 learner의 예측값을 더 의미있게 고려한다)

예를 들어, 5개의 weak learner를 사용하고 각 러너의 성능(=가중치)가 다음과 같이 정해져 있다면

가중치를 반영한 예측값의 총 합계는 -1.3이고 이 값이 음수이기 때문에 최종적으로 -1로 예측한다.
📌 가중치 업데이트 예시
아래와 같이 5개의 데이터 포인트에 대해서 이진 분류를 할 때 가중치는 다음과 같다.

예측값을 바탕으로 틀린 관측치와 맞은 관측치에 대해서 가중치를 업데이트 하면 (여기서 ea1 = 2 라고 가정한다)

따라서 2번 단계에서 가중치는 아래와 같이 업데이트 된다.

위와 같이 업데이트가 된 이후에, 1번 데이터 포인트가 2번 단계에서 sub sample에 뽑힐 확률을 계산하면 아래와 같다.
이 확률을 계산할 때에는 normalize를 바탕으로 계산한다.

따라서 올바르게 예측한 데이터 포인트 1,3,4 의 경우 다시 샘플에 뽑힐 확률이 1/11 이고, 잘못 예측한 데이터 포인트 2.5의 경우 4/11이 된다.
📚 Gradient Boosting
기본적인 gradient boosting과 XGBoost, LightGBM에 대해서 설명한다. 여기서 Gradient는 잔차(=모델이 설명하지 못하는 정도)와 동일한 의미이다.
Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Annals of statistics, 1189-1232.
✅ 기본 개념 설명 : 회귀문제의 경우
이전 단계의 학습기(weak learner)가 종속변수를 설명하지 못하는 정도를 그 다음 단계의 학습기가 보완하는 방식. 즉 이전 단계에서 다음 단계의 오차를 예측해서 더하는 방식으로 학습한다.
회귀 문제를 예시로 각 단계를 설명하면 다음과 같다.
① 첫 번째 학습기를 적용해서 예측값을 구한다. 1단계에서 구한 i번째 관측치에 대한 예측값을 아래와 같이 표현
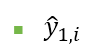
② 1단계에서 구한 예측값과 실제값의 차이를 빼서 잔차를 나타내면 아래와 같다. 즉 r(1,i)는 첫번째 단계에서 적용된 학습기가 i번째 관측치를 설명하지 못하는 정도를 의미한다.
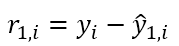
③ 두 번째 학습기는 두 번째 종속변수가 아니라 앞에서 얻은 r1,i를 종속변수로 예측한다. '이전 단계의 학습기가 설명하지 못한 부분을 설명'하는 것이지 '종속변수' 자체를 설명하는게 아니다. 이를 표현하면 아래와 같다.
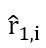
④ ①의 예측치에 ③에서 나온 값을 더해서 두 번째 단계의 종속변수 예측치를 계산할 수 있다.
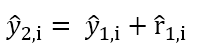
위 방식으로 계속해서 다음 단계의 종속변수 예측값을 계산할 수 있다.
이를 통해서 2번째 단계의 오차를 계산하면, 이 값은 세 번째 단계의 학습기의 종속변수가 된다.
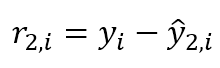
위 식의 풀어서 쓰면 아래와 같이 나타낼 수도 있다 (이 부분은 설명이 왜 나왔는지 애매)
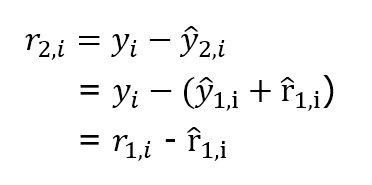
전 단계의 잔차로 예측치를 구하는 과정을 계속해서 반복하면, 최종 예측치를 아래와 같이 일반화된 식으로 나타낼 수 있다.
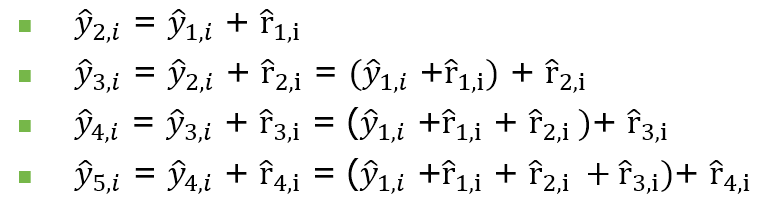

📌학습률 반영
learning rate를 적용하여 예측치를 구할 수도 있다.
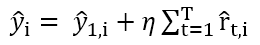
learning rate를 0에 가깝게 하면 개별 학습기가 최종 모델에 미치는 영향력이 줄어들고, 과적합을 감소시킬 수 있다. 단, learning rate가 줄어들수록 T의 크기를 증가시켜서 더 많은 학습기를 사용해야 한다. 따라서 learning rate와 number of etimator는 trade off 관계이다. (하나를 증가시키면 다른 하나는 감소시켜야 함)
📌 Subsample 파라미터
Bagging과 유사하게, 모델을 단게별로 학습할 때 전체 데이터에서 일부를 뽑아서 학습할지를 결정할 수 있다. 이 값이 1이면 전체 데이터를 사용하는 것이고, 0에 가까울수록 조금씩 사용하는 것이다. 이 파라미터를 사용하면 일반화 가능성을 증가시킬 수 있다.
✅ 예시 코드 : 회귀문제
gradient boosting 방식을 직접 구현하는 것과 파이썬 라이브러리를 사용하는 것의 결과를 비교한다. 여기서는 아래와 같은 bike example 데이터를 사용한다.
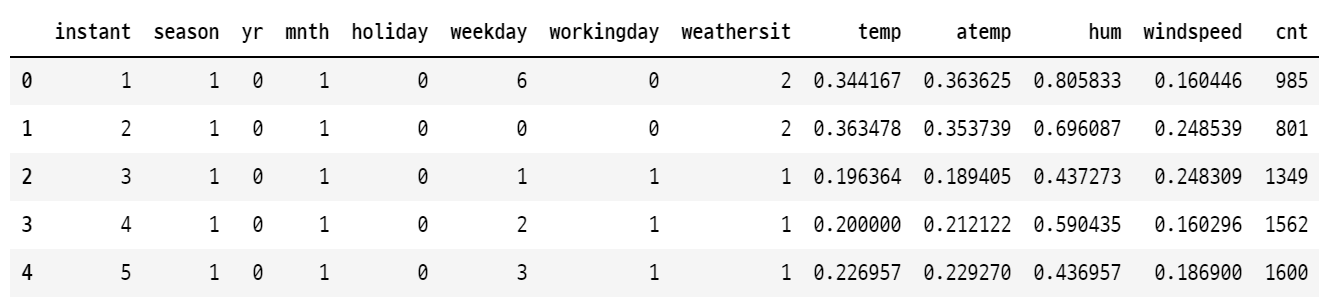
import pandas as pd import numpy as np df_bikes = pd.read_csv('bike_rentals.csv') X_bikes = df_bikes.iloc[:,:-1] y_bikes = df_bikes.iloc[:,-1] from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X_bikes, y_bikes, test_size=0.2)
1. 직접 구현
from sklearn.tree import DecisionTreeRegressor # weak learner 만들기 tree_1 = DecisionTreeRegressor(max_depth=2, random_state=2) ### 1단계 : 학습 tree_1.fit(X_train, y_train) # 1단계에서 종속변수 예측치 계산 y_train_pred = tree_1.predict(X_train) #첫 번째 단계의 종속변수 예측치
첫 번째 단계에서 학습기를 생성하고 종속변수 예측치를 계산한다.( y^ 1,1)
### 2단계 #잔차 계산 y2_train = y_train - y_train_pred #학습기 생성 tree_2 = DecisionTreeRegressor(max_depth=2, random_state=2) #잔차를 종속변수로 학습 tree_2.fit(X_train, y2_train) #두 번째 단계 잔차 예측치 계산 y2_train_pred = tree_2.predict(X_train)
첫 번째 단계의 결과를 이용해서 두 번째 단계에서 예측할 잔차를 구하고 예측을 진행한다.
### 3단계 #잔차 계산 y3_train = y2_train - y2_train_pred #학습기 생성 tree_3 = DecisionTreeRegressor(max_depth=2, random_state=2) # 잔차를 종속변수로 학습 tree_3.fit(X_train, y3_train) # 세번째 잔차 예측치 계산 y3_train_pred = tree_3.predict(X_train)
마찬가지로 세 번째 단계도 진행한다.
#최종 예측값 구하기 y1_pred = tree_1.predict(X_test) #첫 번째 종속변수에 대한 예측치 y2_pred = tree_2.predict(X_test) #두 번째 단계에서 잔차에 대한 예측치 y3_pred = tree_3.predict(X_test) #세 번째 단계에서 잔차에 대한 예측치 y_pred = y1_pred + y2_pred + y3_pred #최종 예측치
최종 예측 결과를 산출한다. 첫 번째 단계에서 구한 종속변수의 예측값에, 그 뒤 단계에서 구한 잔차들은 하나씩 더한다.
2. 라이브러리 사용
from sklearn.ensemble import GradientBoostingRegressor #1부분과 동일하게 맞추기 위해서 depth=2, 학습기 수는 3개로 함 gbr = GradientBoostingRegressor(max_depth=2, n_estimators=3, random_state=2, learning_rate=1.0) gbr.fit(X_train, y_train) # Predict test data y_pred = gbr.predict(X_test)
라이브러리를 사용하면 비교적 간단하게 계산할 수 있다.
1 방식과 비교하기 위해서 MSE를 계산해보면 동일함을 알 수 있다.
✅ 기본개념 설명 : 분류문제의 경우
https://tyami.github.io/machine%20learning/ensemble-5-boosting-gradient-boosting-classification/
https://blog.paperspace.com/gradient-boosting-for-classification/
📚 XGBoost (eXtreme Gradient Boosting)
병렬 연산을 통해서 학습 속도와 성능을 개선시킨 모델이다.
https://arxiv.org/pdf/1603.02754.pdf
https://xgboost.readthedocs.io/en/latest/tutorials/model.html
과적합 문제를 감소시키기 위한 대표적인 방법이 규제화이다. XGBoost는 전체 estimator의 수를 regularization term처럼 비용함수에 포함시킨다. 이를 통해서 전체 모델의 복잡도를 감소시킨다.
또한 모형의 수와 각 leaf node의 종속변수에 대한 기여 정도를 학습해서 최적의 값을 찾는다.

✔ XGBoost 파라미터 설명
https://xgboost.readthedocs.io/en/stable/parameter.html
📚 LightGBM (Light Gradient Boosting Model)
공식 문서 : https://lightgbm.readthedocs.io/en/latest/
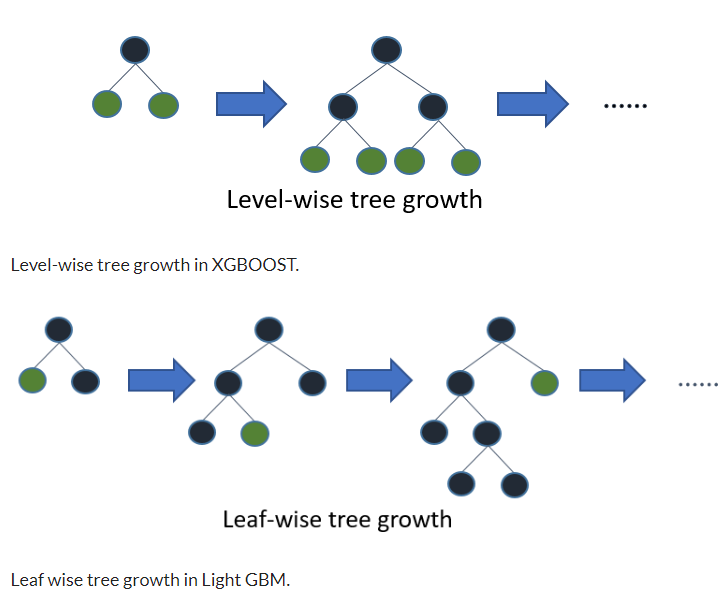
2017년 처음 제안된 부스팅 알고리즘이다. 이전 부스팅 알고리즘은 Leaf-wise split 방식으로 노드가 내려가면서 각 레벨마다 노드를 동일하게 split 했다. 반면 LGBM은 노드의 level은 고려하지 않고 모든 leaf node 중에서 오차 감소에 가장 큰 기여를 하는 노드를 먼저 split 했다.
또한 LGBM은 GOSS(Gradient_based One_Side Sampling)라는 sub-sample 방식을 사용한다. GOSS는 잔차의 절대값 크기를 기준으로 이전 단계에서 분류가 제대로 잘 되었는지 파악한다. 잔차가 클수록 모델의 설명력이 낮음을 의미한다. 따라서 잔차 값이 클수록(=gradient 가 클수록) sub-sample에 포함될 확률이 높아진다.
📚 Catboost (Category Boost)
일반적으로 분류문제에서 범주형 변수는 더미변수화를 시켜야 한다. 이러한 방식이 비효율성을 개선하기 위해서 별도의 방식을 사용했다. 독립/종속변수가 범주형 변수인 경우에 유용함.
세부 설명 :
https://thaddeus-segura.com/catboost/
📚 서로 다른 학습기로 앙상블 하기
분류문제:
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.VotingClassifier.html
회귀문제 :
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.VotingRegressor.html
Python에서는 VotingClassifier를 사용해서 서로 다른 알고리즘을 weak learner로 사용해서 앙상블 모델로 결합할 수 있다.
분류문제의 경우 voting = hard/soft 를 선택한다. hard 방식의 경우 다수결로 최종 예측 클래스를 정하고, soft 방식은 개별 분류기가 산출하는 각 클래스에 대한 확률값을 더해서 최종 예측 클래스를 정한다.
회귀 문제의 경우 평균값을 최종 예측치로 사용하기 때문에 voting 파라미터를 사용하지 않는다.
from sklearn.linear_model import LogisticRegression from sklearn.naive_bayes import GaussianNB from sklearn.ensemble import RandomForestClassifier, VotingClassifier clf1 = LogisticRegression(multi_class='multinomial', random_state=1) clf2 = RandomForestClassifier(n_estimators=50, random_state=1) clf3 = GaussianNB()
로지스틱회귀, 랜덤 포레스트, 나이브 베이즈를 결합하는 앙상블 모델을 만든다.
## Hard Voting eclf1 = VotingClassifier(estimators=[ ('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard') ## Soft Voting eclf2 = VotingClassifier(estimators=[ ('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft') ## 가중치 부여 eclf3 = VotingClassifier(estimators=[ ('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft', weights=[2,1,1])
voting 파라미터를 통해서 hard / soft voting 방식을 선택할 수 있다. weight 파라미터를 이용하면 각 학습기의 가중치도 부여할 수 있다.
📚 Reference
https://velog.io/@jiselectric/Ensemble-Learning-Voting-and-Bagging-at6219ae
https://en.wikipedia.org/wiki/Bootstrap_aggregating
H. Guo et al. (eds.), Manual ofDigital Earth, https://doi.org/10.1007/978-981-32-9915-3_10
https://en.wikipedia.org/wiki/Boosting_(machine_learning)
https://arxiv.org/pdf/1603.02754.pdf
https://www.analyticsvidhya.com/blog/2017/06/which-algorithm-takes-the-crown-light-gbm-vs-xgboost/
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| 차원축소 - PCA(Principal Component Analysis) (0) | 2022.05.30 |
|---|---|
| 차원축소 기본 - 고유값, 고유벡터, 고유분해 (0) | 2022.05.29 |
| 앙상블 기법(Ensemble Method) - Bagging (0) | 2022.05.24 |
| 의사결정나무 (Decision Tree) (0) | 2022.05.24 |
| 나이브 베이즈 (Naive Bayes) (0) | 2022.05.15 |




댓글