📚 PCA(주성분 분석)
✅ Principal Component 개념
• PCA는 Feature extraction 방법 중 하나이다. Principal component는 하나의 벡터인데, 이는 독립변수들이 가지고 있는 정보(분산으로 표현)를 설명하는 축을 의미한다.
• 전체 PC의 수 = 전체 독립변수 수
• 각 PC가 설명하는 정도가 다 다르기 때문에, 분산을 설명하는 큰 PC를 새로운 feature로 선택해서 사용할 수 있다.
→ 원 데이터의 정보(분산)의 손실을 최소화하면서 피쳐의 수를 감소시킬 수 있다.
📌예시 1

예를 들어 위와 같이 총 피쳐가 5개이고 각 피쳐의 분산의 크기에 따라서 정렬하고, 설명력이 높인 상위 두개의 PC인 PC1, PC2를 선택했다고 하자. 이를 통해서 피쳐의 수를 5개 → 2개로 감소시킬 수 있고, 원본 데이터의 정보 중 95%를 사용할 수 있다.
📌 예시 2
독립변수의 수가 2개(=PC의 수가 2개)인 경우,
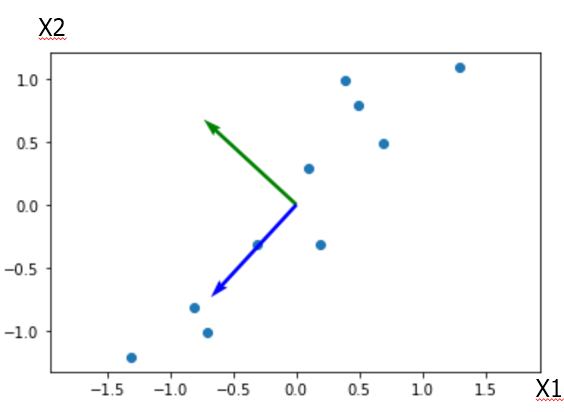
위와 같이 표현할 수 있다. 관측치들이 대각선 방향으로 가장 많이 분산되어 있기 때문에 첫번째 PC는 분산을 가장 많이 설명하는 파란색 축이 된다. 두번째 PC는 첫번째 PC와 수직인 축 중에서 가장 많은 분산을 설명하는 초록색 축으로 표현될 수 있다. PC는 분산(정보)를 설명하는 축이고, 분산은 데이터가 흩어진 정도를 나타낸다.
이 예시에서는 PC가 2개이므로, 차원을 축소하기 위해서는 파란색 축을 새로운 피쳐로 선택해서 피쳐의 수를 줄이고 설명력을 최대한 확보한다.
✅ PCA 순서
PC를 찾기 위해서는 고유값, 고유벡터, 고유분해를 사용한다. PCA 순서는 다음과 같다.
① 각 피쳐에 대해서 Mean centering을 실시한다. Mean centering value = 원래 값 - 평균
② 원래 데이터의 공분산 행렬을 계산한다.
공분산 행렬은 정사각/대칭 행렬이고, k개의 피쳐가 있으면 k x k 형태가 된다.
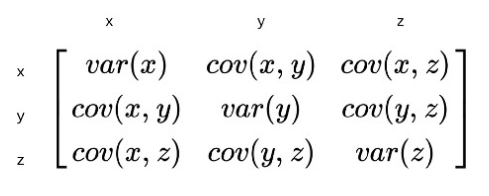
• 공분산 행렬에서 자기 자신과의 공분산(=대각행렬)은 분산이 된다.
③ 공분산 행렬에 대해서 고유값과 고유벡터를 찾는다 → 고유벡터가 PC가 됨
• 특정 행렬에 대한 고유값, 고유벡터를 구하는 방법은 이전 포스트 참고(차원축소 기본 - 고유값, 고유벡터, 고유분해)
• 어떤 행렬이 대칭이면, 해당 행렬에 대한 고유 벡터는 서로 수직인 관계를 가진다. 따라서 공분산 행렬에서 도출되는 PC들도 서로 수직이다.
④ 그 중에서 설명력이 높은 PC만 선택한다.
• 각 PC들의 분산의 크기(=설명력)는 각각의 벡터에 대한 고유값으로 알 수 있다.
피쳐가 k개가 있으면 고유값(λ)도 k개가 존재한다. 각 λ의 크기를 확인하기 위해서는 전체 데이터의 k개의 피쳐들의 분산을 먼저 계산해야 한다. 전체 분산의 크기는 아래와 같이 계산한다.

• 이러한 전체 분산의 크기는 공분산 행렬의 대각 성분의 합(=해당 행렬의 trace)으로 구할 수 있다.
공분산 행렬의 대각성분의 합 = Trace = 고유값의 합
고유값은 해당 고유벡터에 의해서 설명되는 분산의 크기를 의미한다. λ1=var(x1), λ2=var(x2), λ3=var(x3) .... 와 동일한 의미이다. 따라서 PC들 중에서 어떤 것을 선택할 지는 λ의 값이 큰 것부터 기준으로 정할 수 있다.
⑤ 새로 선택한 PC에 대해서 기존 관측치의 새로운 값을 구한다.
새로운 축(PC)를 선택했으므로, 기존 변수들을 해당 PC에 대해서 새롭게 정의해야 한다.
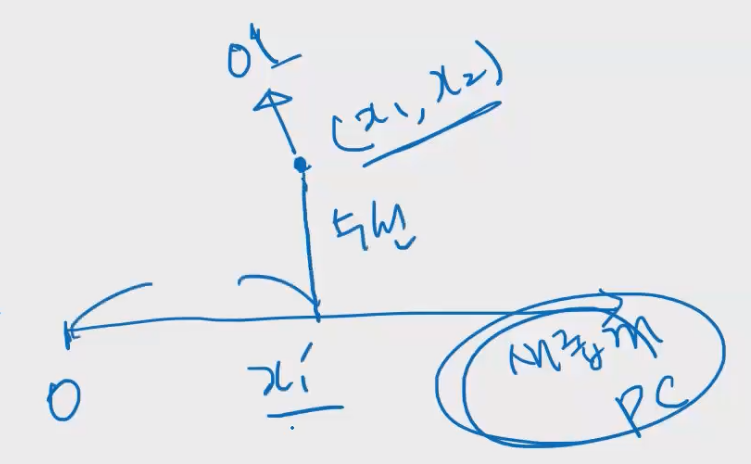
원래 관측치가 x1, x2라는 두 개의 피쳐로 표시될 때, PCA를 실행해서 새로운 PC 1개를 구하면 일차원 상의 직선으로 나타낼 수 있다. 여기서 원래의 관측치를 새로운 PC에 맞춰서 업데이트 하기 위해서, 새로운 축에 수선을 내리고 원점으로부터의 거리를 계산하면 새로 도출한 PC에 대한 값인 x1' 를 구할 수 있다.
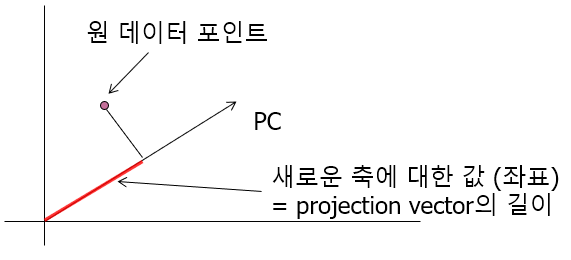
만약 PC가 2개라면 위와 같이 나타낼 수 있다. 이렇게 PC를 이용해서 관측치를 표현하는 것을 projection vector를 이용해서 설명하면 아래와 같다.

위에서 원래 관측치를 추출한 PC에 맞게 업데이트 하기 위해서는 𝑥 ⃗1 벡터의 값을 알아야 한다. 이 벡터는 원점으로부터 수선과의 교점가지의 거리를 나타내고 projection vector라고 부른다. 𝑥 ⃗1 를 식으로 나타내면 아래와 같다.
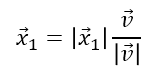
벡터의 방향을 나타낼 때에는 단위벡터를 사용한다. 단위벡터는 길이가 1인 벡터인데, 일반적으로 길이가 아니라 방향이 중요한 경우에 단위 벡터를 이용해서 표현한다. 특정 벡터를 해당 벡터의 길이로 나누면 단위벡터가 된다. 따라서 위 식은 길이가 𝑥 ⃗1과 같고 방향은 𝑣 ⃗ 의 단위벡터와 동일한 벡터를 의미한다.
이 값을 구하기 위해서 코사인 세타를 활용한다.
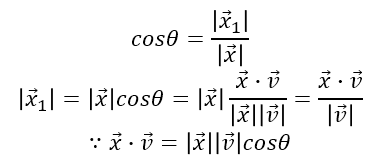
위 식에서 두번째 줄 마지막 분모의 v는 PC의 고유벡터이므로 길이가 1이다(이전 포스트 참고) 따라서 분자만 남게된다.
결과적으로 𝑥 ⃗1는 원래 관측치의 벡터와 새로운 PC의 고유벡터의 내적으로 구할 수 있다. 즉 원 데이터의 벡터와 새로운 PC의 벡터를 곱해서 새롭게 업데이트 된 좌표를 구할 수 있다.
✅ 코드로 살펴보기
import numpy as np
import pandas as pd
d = pd.read_csv('pca_data.csv', header = None)
d_np = d.values
임시 데이터를 가져온다. 이 데이터는 피쳐가 2개로 구성되어 있고 관측치는 10개 이다.
# mean centering 실시
m = d_np.mean(axis = 0)
centered_d = d_np - m
# 공분산행렬 구하기
cov_m = np.cov(centered_d.T) #transpose해서 넣어야 함
# 대각성분만 뽑아내기
np.diag(cov_m)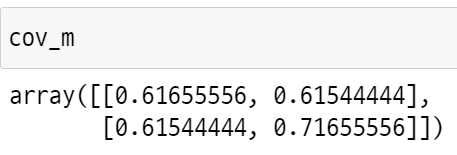
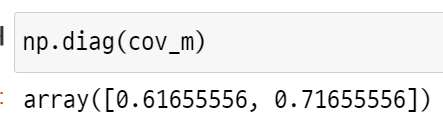
피쳐의 수가 2개이므로 공분산 행렬도 2x2 형태이다. 여기서 대각성분들은 각 피쳐의 분산을 설명하는 정도(=고유값)이 된다. 대각 성분을 모두 더하면 원래 피쳐들의 분산정도를 계산할 수 있다.
#고유값, 고유벡터 구하기
eigvalues, eigvectors = np.linalg.eig(cov_m)
eigvalues
np.sum(eigvalues)#1.28402771+0.0490834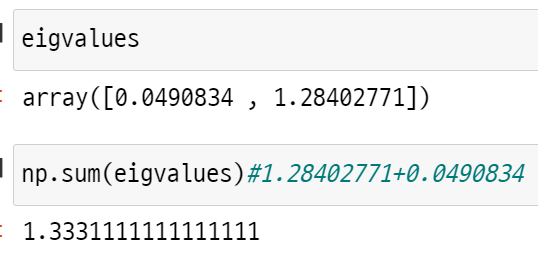
공분산 행렬의 고유값과 고유벡터를 구한다
② 고유값들의 합 = 행렬의 trace = 대각 성분의 합 = tr(행렬) *(이전포트스 참고)
이므로 eigvalues를 더한 값은 cov_m의 대각성분의 합과 동일하다. 고유값은 각 고유벡터에 대한 분산의 크기를 나타내는데, 이 데이터의 전체 분산은 1.33이고, 각 피쳐의 분산의 정도는 0.04, 1.28임을 알 수 있다.
1.28/1.33=0.963 이기 때문에 두 번째 피쳐만 사용해도 원래 데이터의 정보 중에서 96% 가량을 사용할 수 있다.
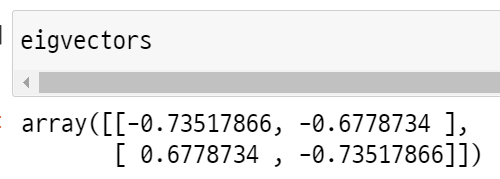
고유벡터는 위와 같은데, 첫 번째 열의 고유값은 0.04, 두 번째 열의 고유값은 1.28이다. 따라서 두 번째 고유 벡터의 PC를 선택하는 것이 바람직하다.
import matplotlib.pyplot as plt
plt.plot(centered_d[:, 0], centered_d[:, 1], 'o', label = 'data')
plt.legend()
plt.show()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(centered_d[:, 0], centered_d[:, 1])
ax.quiver((0,0), (0,0), eigvectors[0,:], eigvectors[1,:],color=['g','b'], units = 'xy', scale = 1)
plt.axis('equal')
plt.show()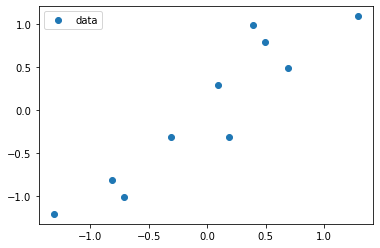
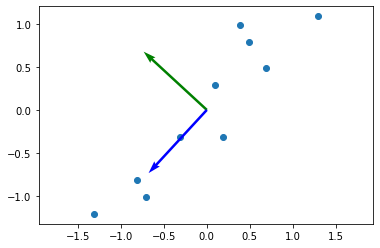
시각화를 해보면 더 많은 분산을 설명하는 파란색 PC가 피쳐2에 해당하는 것임을 알 수 있다.
# 두번째 PC를 선택
F = eigvectors[:,1]
#내적 계산
new_data = np.dot(centered_d, F)
#시각화
plt.plot(new_data,np.zeros(10), 'o', label = 'data')
plt.legend()
plt.show()

PCA를 진행한 두 번째 피쳐를 F로 저장하고, 원래 관측치과 내적을 진행해서 업데이트할 값을 계산한다.
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit_transform(d_np)
파이썬 라이브러리를 이용하면 간단하게 진행할 수 있다.
📚 Reference
'머신러닝, 딥러닝 > 머신러닝' 카테고리의 다른 글
| 서포트 벡터 머신 (Support Vector Machine) (0) | 2022.06.18 |
|---|---|
| 특이값 분해 (Singular Value Decomposition) (0) | 2022.06.17 |
| 차원축소 기본 - 고유값, 고유벡터, 고유분해 (0) | 2022.05.29 |
| 앙상블 기법(Ensemble Method) - Boosting (0) | 2022.05.28 |
| 앙상블 기법(Ensemble Method) - Bagging (0) | 2022.05.24 |




댓글