📚 Probability(확률)
✅ 확률 관련 기본 용어 정리
🏷️ 집합
여러 개의 원소로 구성된 그룹이고, 중복되는 원소를 가질 수 없다.
🏷️ 시행 (Experiment, trial)
동일한 조건에서 반복 수행이 가능하고, 결과를 사전에 알 수 없는 행동.
집합으로 표현된다.
🏷️ 표본공간 (Sample space)
어떤 시행에서 발생 가능한 모든 결과의 집합. 표본공간의 각 원소를 sample point라고 한다.
ex) 주사위를 한 번 던지는 시행의 표본 공간 = {1,2,3,4,5,6}
동전을 한 번 던지는 시행의 표본 공간 = {앞, 뒤}
두 개의 동전을 동시에 던지는 시행의 표본 공간 = { (H,H), (H, T), (T, H), (T, T) }
🏷️ 사건(Event)
시행의 결과로 나타날 수 있는 특정한 값 또는 값들의 집합
= 시행에 대한 표본공간의 부분집합 (수학적 정의)

사건은 집합으로 표현할 수 있는데, 모두 해당 시행에 대한 표본 공간의 부분 집합이다.
✅ 확률
📌 확률의 정의
사건 A가 발생할 확률 P(A)
= 사건 A집합의 원소의 수 / 표본공간의 원소의 수
= 해당 사건이 발생할 경우의 수 / 특정 시행에 대한 모든 가능한 결과에 대한 경우의 수
예시 ) 주사위 두 개를 동시에 던져서 눈의 합이 4보다 작을 확률
• 시행 : 주사위를 두개 동시에 던짐
• 사건 : 나온 두개 주사위의 합이 4보다 작음 : E = { (1,1), (1,2), (2,1) }
• 표본공간 : S = { (1,1), (1,2), (1,3)..... (6,6) }
📌 확률 관련 명제 (Axioms)

📌교집합과 합집합의 표현

✅ 독립 사건 (Independent events)
사건 A,B가 독립인 경우 사건 A 가 발생학 확률은 사건 B가 발생할 확률에 영향을 미치지 않음

📌 상호 배타적 vs 상호독립적
상호 배타적 : 교집합이 0이다 = 두 사건이 동시에 발생하지 않는다

✅ 조건부 확률 (Conditional probability)
두 개의 사건 A, B에 대해서, 사건 B가 발생한 조건 하에서 사건 A가 발생할 확률

📌 조건부 확률 관련 명제

✅ 전체 확률의 법칙(Law of total probability)

B1, B2, B3은 S의 파티션이라고 한다. 파티션 B들의 특징은 다음과 같다.
1. 서로 상호배타적이므로 교집합이 없다
2. 모두 더하면 표본공간인 S이다.
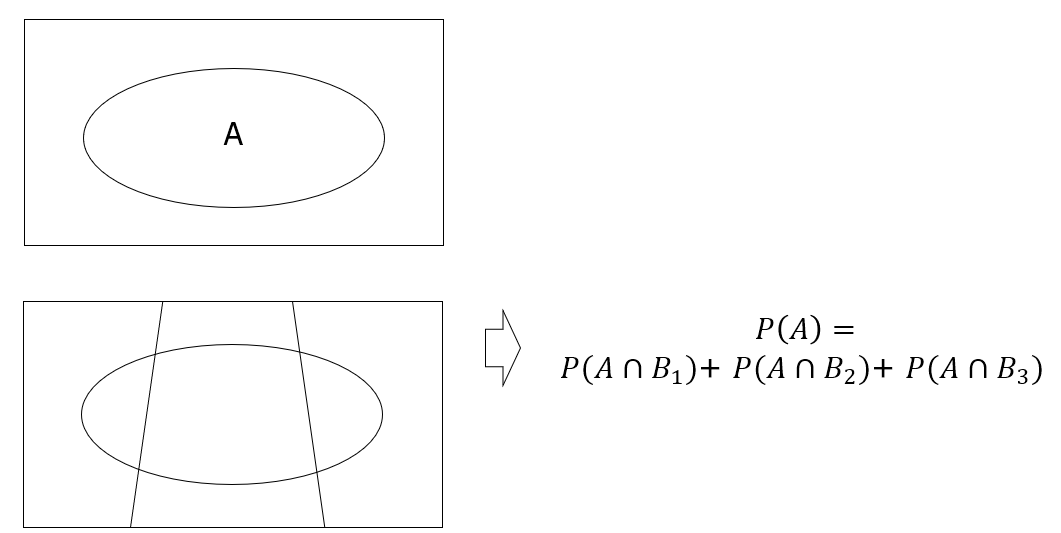
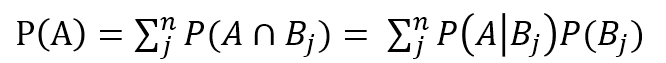
전체 확률의 법칙은 특정 확률의 사건(A)을 표본 공간의 파티션으로 표현한 것을 의미한다. B1, B2, B3이 S의 파티션이라면 위의 식처럼 표현할 수 있다.
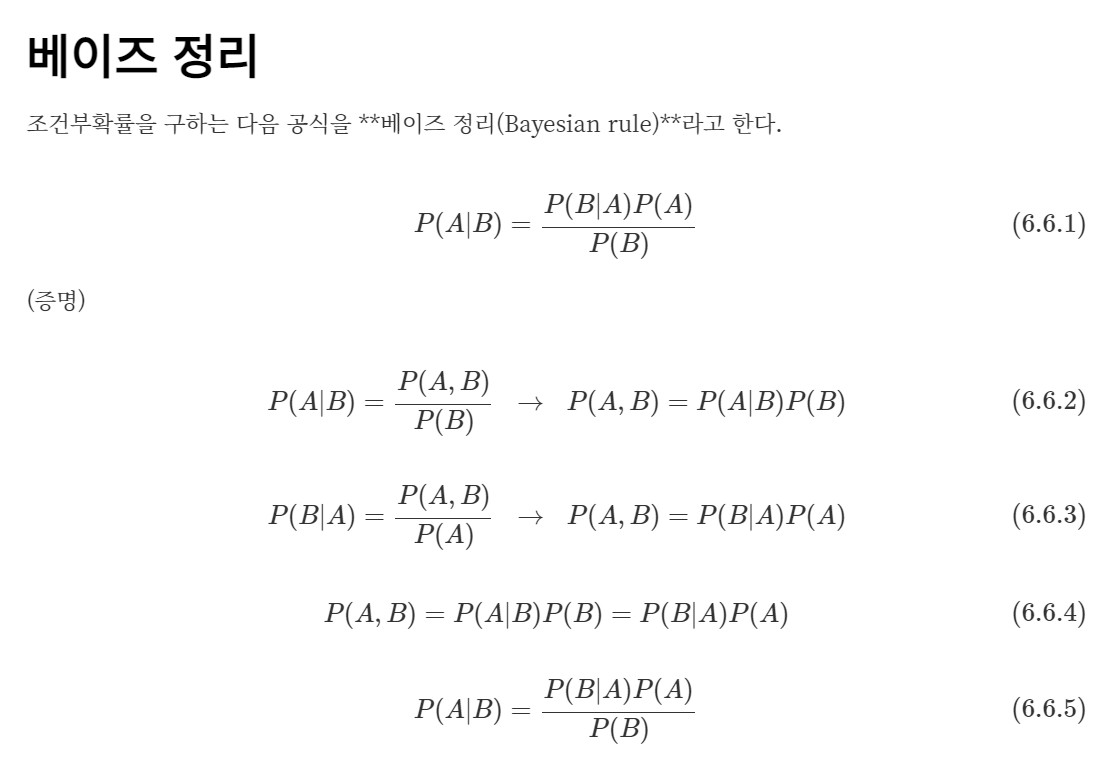
✅ 베이즈 정리 (Bayes' Theorem)
베이즈 정리 설명 잘 되어있는 사이트 :
6.6 베이즈 정리 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
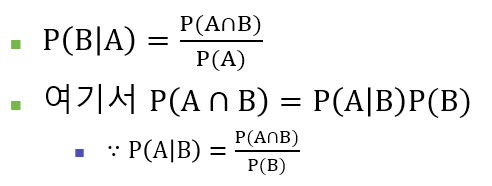
조건부 확률을 위와 같이 나타낼 수 있는데,

이렇게 나타낸 것이 베이즈 룰이다. marginal probability(주변 확률)을 사용하면 아래의 두 가지 식으로 나타낼 수 있는데 이것이 나이브 베이즈 알고리즘의 기본이 된다.
다른 자료 )
📌 베이즈 정리의 확장
위에서 도출한 베이즈 정리를 확장하면 multi-class classification에 사용할 수 있다. 전체확률 정의에 따라서 분모를 각 클래스에 대한 확률로 재 정의하여 작성할 수 있다.
자료 1.

자료 2.
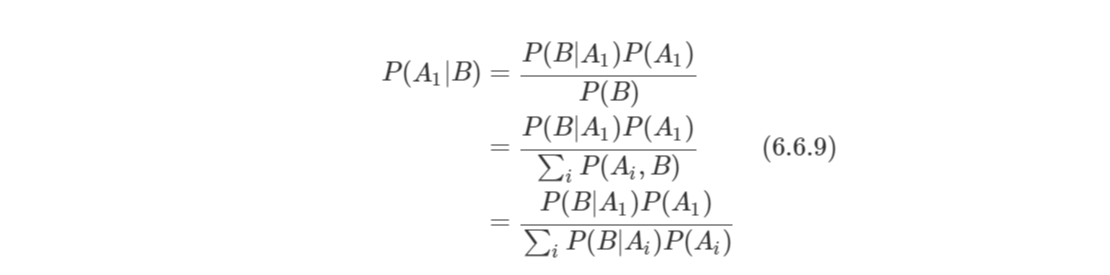
B라는 사건이 발생했을 때, A1/A2/A3/A4가 발생활 확률을 베이즈 정리로 계산하면 아래와 같다.
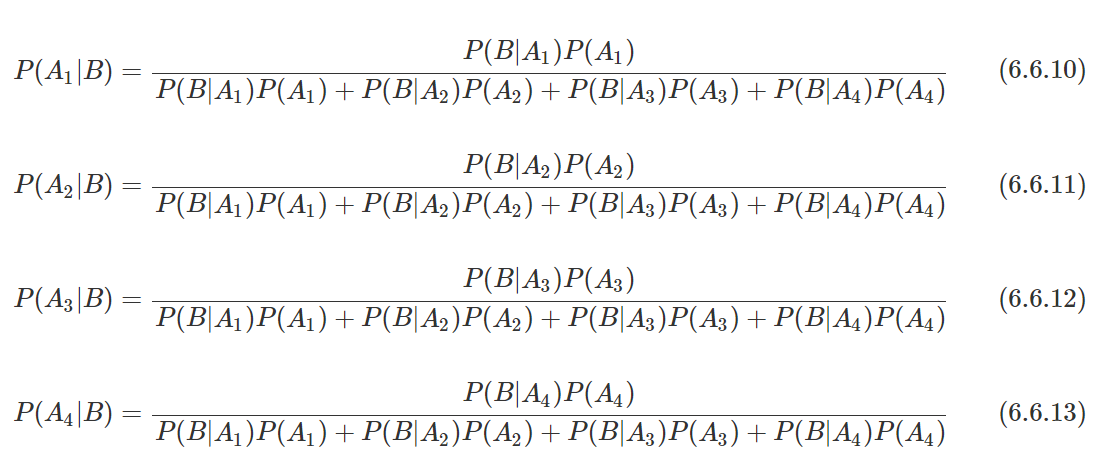
✅ 확률에서의 변수 (Random Variable)
정의 : 무작위 시행(random experiment)의 결과에 의해서 결졍되는 값
예시 : 두 개의 동전을 동시에 던지는 시행의 표본 공간 : S = {(H,H), (H, T), (T, H), (T, T)})}
이러한 관점에서 변수는 하나의 숫자를 무작위 시행의 결과에 할당하는 함수라고 생각할 수 있다.

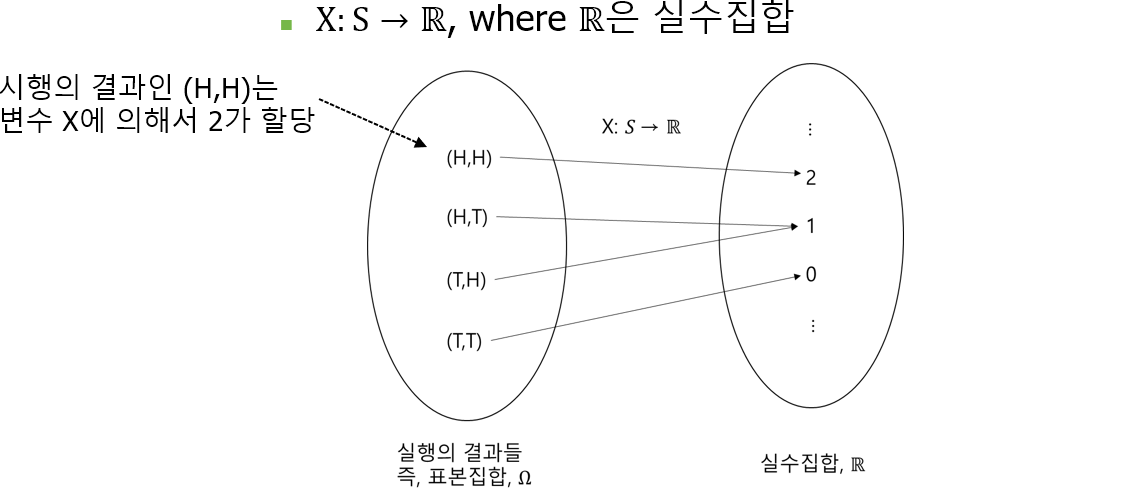
변수가 특정한 값을 취하는 것은 하나의 사건으로 간주할 수 있음. 변수는 위의 그림과 같이 동전의 앞 뒤가 나오는 여러 사건들이 모여있는 확률의 '표본 공간'을 '실수'로 변환하는 함수라고 볼 수 있다.
✅ 확률에서의 변수의 종류 : 이산 변수 vs 연속 변수
📌이산 변수 : 셀 수 있는 변수
1. Finite
변수의 값이 finite 한 변수이다.
ex) 성별, 정치성향(진보/보수/중도), 자동차 바퀴 수 등
2. Countably Infinite
이론적으로는 값이 무한대이지만 실제로는 카운트가 가능한 변수.
ex) 1년에 백화점에 방문한 사람 수, 연간 교통사고 수
📌연속 변수 : 셀 수 없는 변수
무한하고 셀 수 없는 변수로, 특정 구간에 존재하는 모든 값을 다 취할 수 있다.
간단하게는 소수점을 취할 수 있는 변수라고 볼 수 있다.
ex) 온도, 무게, 길이 등의 단위.
온도의 경우 10도와 11도 사이에 무한히 많은 값이 존재한다.
✅ 이산 변수의 확률
확률 질량 함수(probability mass function)를 사용한다. 확률 질량 함수는 이산 변수가 특정한 값을 취할 확률을 나타낼 때 사용되는 함수이다.
취할 수 있는 값들이 {𝑥_1,𝑥_2,𝑥_3, …}인 이산변수 X에 대해서 다음과 같이 표현 가능. 일반적으로 변수마다 PMF는 다르다.
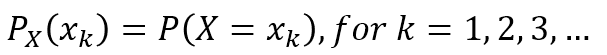

가장 마지막 줄에 있는 확률 표현을 변수 X에 대한 PMF라고 한다.
📌 이산 변수의 확률분포
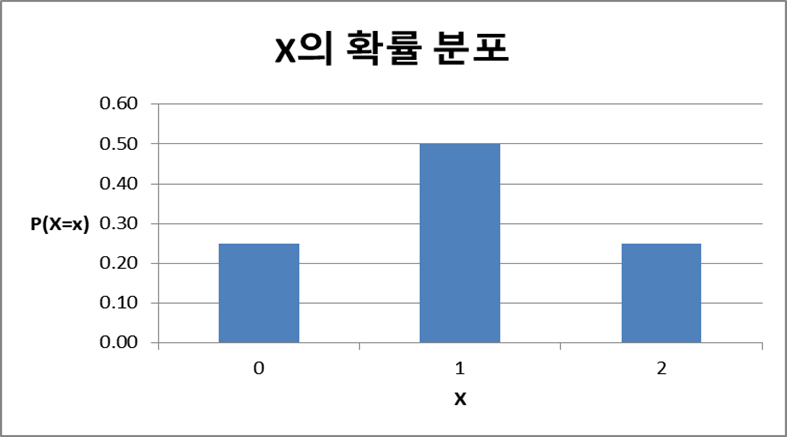
확률분포 : 하나의 변수가 취할 수 있는 값과, 각 값을 취할 확률을 대응시켜 둔 것.
이산 변수에 대해서는 pmf를 확률분포라고도 한다.
pmf를 안다는 것은 변수가 각 값을 취할 확률을 안다는 것을 의미하기 때문.
대표적인 이산 확률분포의 예시는 다음과 같다.
🏷️베르누이 분포 (Bernoulli Distribution)
한 번 시행을 했을 때 나오는 결과가 두 개인 경우 (=변수가 취할 수 있는 값이 0 or 1 인 경우) 해당 분포를 베르누이 분포라고 한다.
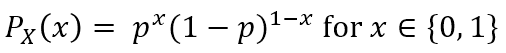
베르누이 분포의 pmf를 위와 같이 나타낼 수 있다.
🏷️이항 분포 (Binomial Distribution)
한 번 시행으로 나올 수 있는 값이 1 or 0인 시행을 반복해서 n번 수행할 때 나오는 1의 수를 값으로 취하는 변수가 이항 변수이다.
즉, 베르누이 분포를 n번 누적한 것이라고 볼 수 있음.
그리고 이 변수가 취할 확률을 pmf로 계산한 것이 이항 분포이다.

(n, x)는 nCx를 의미한다. (combination)
🏷️결합 확률 질량 함수 (Joint probability mass function)
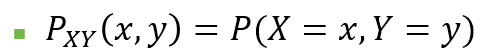
두 개의 이산 변수가 있을 때, 변수 X가 x 값을 가지고 동시에 변수 Y가 y값을 가질 확률을 위처럼 표시함.
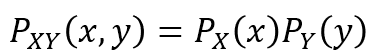
만약 서로 독립인 경우에는 위와 같이 독립인 두 사건을 계산하는 확률과 동일하게 표현할 수 있다.
✅ 연속 변수의 확률
확률 밀도 함수 (probability density function : pdf)를 사용한다.
연속 변수의 경우 변수가 가질 수 있는 값이 무한히 많다. 따라서 연속 변수가 하나의 특정한 값을 가질 확률은 0으로 정의되며 별로 중요하지 않다. 대신에 변수가 특정 구간 사이의 값을 가질 확률이 중요하다.
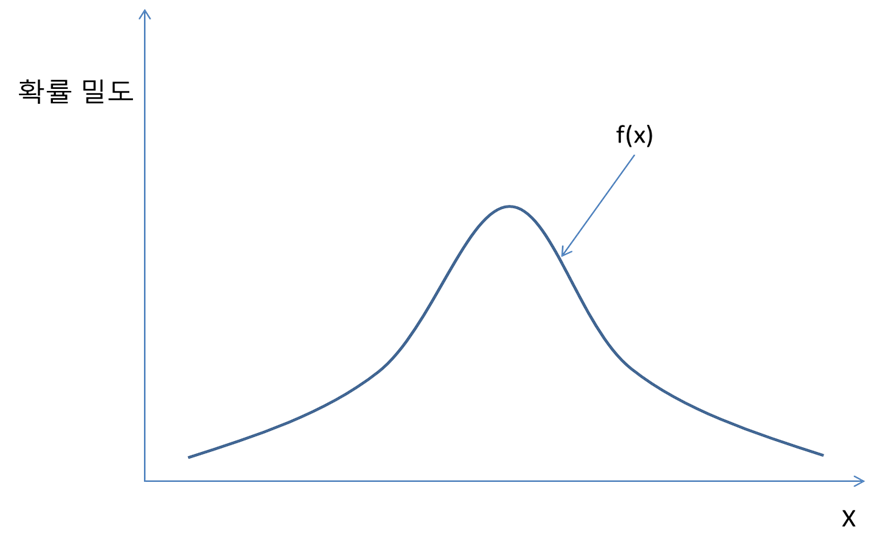
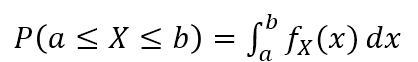
이산 변수와 달리 특정 구간의 값을 취할 확률을 그래프상의 면적으로 나타낸다. 위 식에서 f(x)를 PDF라고 한다.
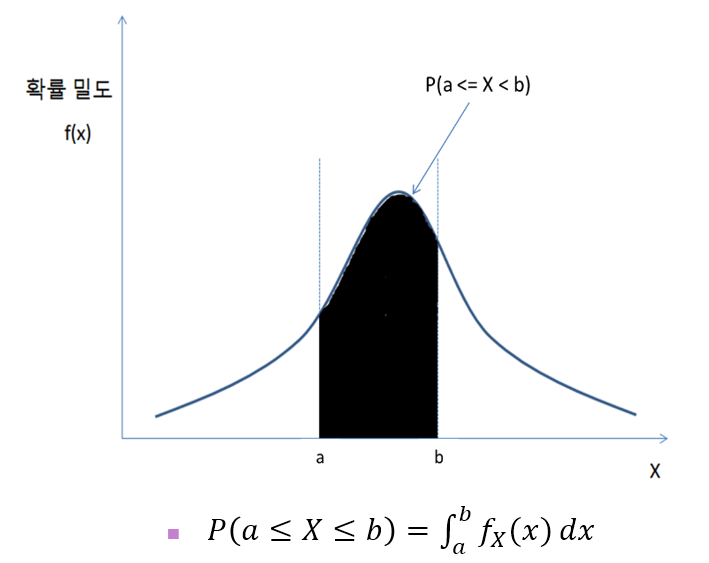
위와 같이 특정 '구간'이 확률을 나타내기 때문에, f(b)와 같은 특정 지점은 확률의 의미를 가지고 있지 않다.
🏷️ 누적 분포 함수 (cumulative distribution function : cdf)
: 변수가 특정 값 이하를 취할 확률을 나타내는 함수로, 0~1 사이의 값을 가진다.
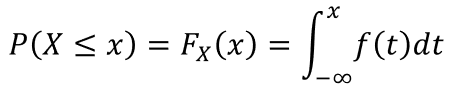
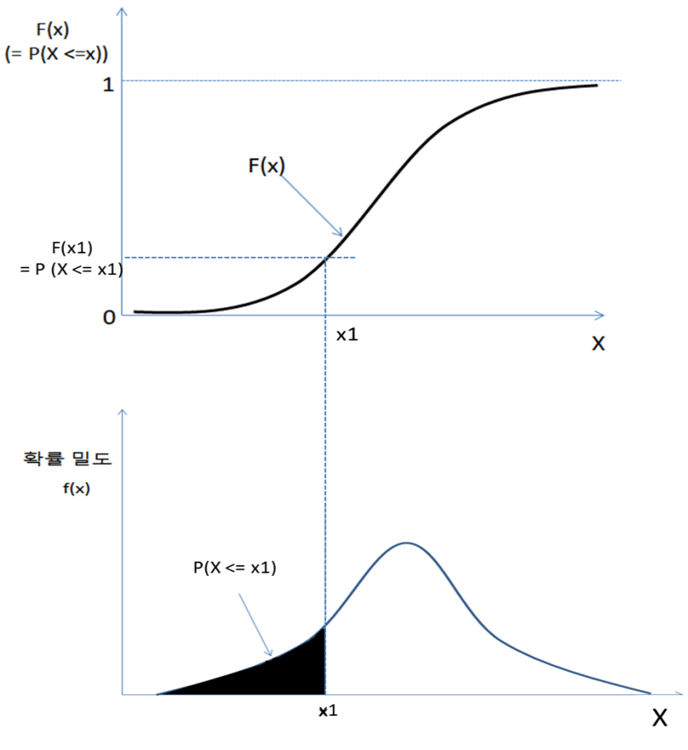
위 그림과 식은 연속 변수의 CDF를 나타낸 것이다.
✅ 평균 / 분산 / 공분산 / 상관계수 / Moment
변수에 대한 확률 분포를 파악하기 위해서는 분포의 형태와 위치를 아는 것이 중요하다. 분포의 형태와 위치에 영향을 주는 것은 평균과 분산이 있다.
📌 평균 (분포의 평균)
• 0에 대한 1차 moment이다.
• 이산 변수와 연속 변수에 대한 평균은 위와 같이 다른 식으로 계산된다.

• 평균 관련 특성
마지막 : 자기 자신을 조건으로 걸면 상수 X로 반환됨
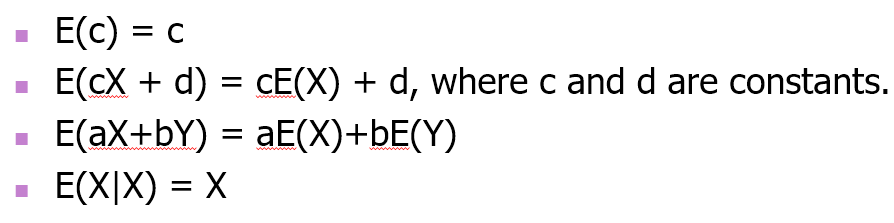
📌 분산 (Variance)
• 분포의 퍼진 정도를 나타낸다.
• 평균에 대한 2차 moment이다.
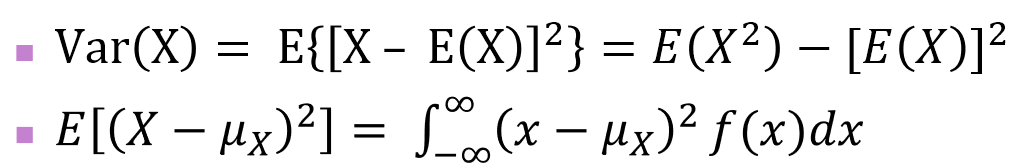
위의 두 번째 식은 평균 continuous RV 부분의 두 번째 식을 통해서 유도 가능.
첫 번째 식 유도 과정은 아래와 같음. (μ = E(x)라서 대치 가능)

• 분산과 관련된 특성들.
분산에 상수를 더하는 것은 아무런 영향을 미치지 않으며, 상수를 곱할 경우에는 제곱으로 밖으로 나온다.
마찬가지로 자기 자신에 대한 조건을 걸면 상수로 반환된다.
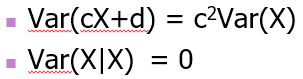
📌 공분산 (covariance)
• 정의 : 서로 다른 두 변수의 값이 변하는 정도
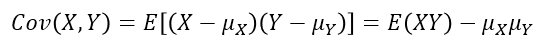
식 유도 :
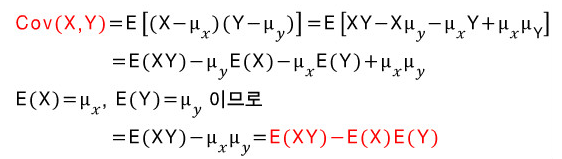
X, Y가 독립이면 E(XY)=E(X)E(Y)=μX*μY 이라서 Cov(X,Y) =0 이다.

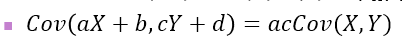
📌 상관계수 (Correlation Coefficient)
• 정의 : x, y 두 변수의 공분산을 x,y 표준편차로 나눈 것 (공분산을 표준화한 것)
• -1 ~ 1 사이의 값을 가진다
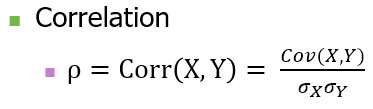
✅ Moment
• 정의 : A moment is a specific quantitative measure of the shape of a function
확률분포 또는 pdf의 형태를 결정하는 값을 모멘트라고 한다.
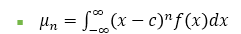
상수 c에 대한 n차 모멘트는 위와 같이 나타낼 수 있음.

•평균은 숫자 0에 대한 1차 모멘트이다. 위 식에서 c=0, n=1 일 때 평균 식과 동일하게 나타난다.
•분산은 평균에 대한 2차 모멘트이다. c=μ, n=2 일 때 분산 식과 동일함.

3,4차부터는 시그마의 n승으로 나눈 표준화된 모멘트를 사용한다.
왜도는 평균에 대한 3차 moment이다. n=3, c=μ이다.
첨도는 평균에 대한 4차 moment이다. n=4, c=μ이다.
📚 Reference
이상엽, 연세대학교 언론홍보영상학부 부교수, 22-1학기 기계학습 이론과 실습
데이터 사이언스 스쿨
존이님 네이버 블로그
https://blog.naver.com/PostView.naver?blogId=mykepzzang&logNo=220838462884&redirect=Dlog&widgetTypeCall=true&directAccess=false
'데이터 분석 > 통계, 분석기법' 카테고리의 다른 글
| 교차 엔트로피(Cross Entropy) (0) | 2022.04.11 |
|---|---|
| 다변량 확률 분포, Maximum Likelihood Estimator (0) | 2022.04.10 |
| Association Rules - 장바구니 분석 (0) | 2021.11.24 |
| 생존분석(Survival Analysis) : Kaplan-Meier / Cox Proportional Hazard / BYTD (0) | 2021.11.15 |
| VAR (Vector Auto Regressive) 모형 (0) | 2021.11.01 |


댓글