📚 Multivariate Probability Distribution
✅ 결합확률분포 : Joint probability distribution
• 변수가 2개 이상일 때, 변수들이 취할 확률 값을 계산하기 위한 확률 분포
• Joint probability is a statistical measure that calculates the likelihood of two events occurring together and at the same point in time

두 개 변수에 대한 이산확률분포, 연속확률분포를 위와 같이 나타낼 수 있음

X는 동전 던질 때의 사건, Y는 주사위를 던질 때의 사건이다. (X, Y는 독립)
각 셀은 X,Y 두 변수에 대한 결합확률 분포를 나타낸다.
✅ Marginal probability distribution : 주변확률분포
정의 : 다른 변수가 어떤 값을 취하는지와 상관없이, 관심이 있는 변수가 어떤 값을 취할 확률
ex) 위 표에서 동전이 앞면이 나올 확률과 상관없이 주사위가 1이 나올 확률

이산변수의 경우 Y 값에 상관없이 X=x일 확률을 위와 같이 표현할 수 있다.
이는 Y가 취할 수 있는 각 값에 대해서 X와 Y의 결합확률의 합을 의미한다. 즉, 이산변수인 경우에는 결합확률을 이용해서 주변확률 분포를 구할 수 있다.
예제 ) 결합확률로 주변확률 구하기
위의 예제(X=동전 던지기, Y=주사위 던지기)에서 X=H에 대한 주변확률을 계산하면 아래와 같다.


연속변수의 경우 적분을 통해서 주변확률분포를 구한다.
1번 식 : X에 대한 주변확률을 구하기 위해서는, X,Y의 결합확률을 Y에 대해서 미분한다.
2번 식 : Y에 대한 주변확률을 구하기 위해서는, X,Y의 결합확률을 X에 대해서 미분한다.

📚MLE (Maximum Likelihood Estimatator : 최대우도추정방법 )
• 정의 : 파라미터의 값을 계산하는 과정을 추정(estimation)이라고 한다. 최적의 방식으로 추정을 할 때 사용하는 방식 중 하나가 MLE이다. MLE는 likelihood를 최대화하는 파라미터를 찾는 과정을 의미한다.
likelihood는 우리가 가지고 있는 데이터의 확률을 의미하며, 머신러닝 에서는 주로 종속변수에 대한 확률로 사용된다.
선형 모형의 OLS는 비용함수인 MSE를 최소화하는 방식으로 파라미터의 최적 값을 탐색한다.
하지만 비선형 모델에서는 OLS를 사용하지 않고 MLE를 사용한다. 비선형 모형의 예시는 Logistic Regression가 있다.

위 식은 표준 로지스틱 분포의 cdf 이다. 즉 우변의 식을 이용해서 Y=1일 확률을 구한다.

파라미터가 종속변수와 선형 관계인 경우에 선형 모델이라고 하는데, 위의 로지스틱 분포의 경우 파라미터 z가 종속변수와 비선형 관계이다.
이러한 파라미터를 찾을 때 사용하는 방식이 MLE 이다. MLE는 likelihood 값을 maximize하는 파라미터 값을 찾는다.
MLE를 이용해서 만든 것이 대표적으로 classification에서 사용되는 교차 엔트로피이다.

✅ Likelihood 란?
• 정의 : 우리가 가지고 있는 데이터의 확률(ex. 종속변수)을 의미한다.
likelihood는 우리가 관심이 있는 종속변수의 확률 분포를 이용해서 표현한다. 일반적으로 종속변수의 특성에 따라(이진 변수 등) 적절한 확률 분포가 정해져 있다.
likelihood는 joint probability를 이용해서 표현한다.

데이터에 n개의 관측치가 있고 종속변수 y인 경우에는 첫 번째 줄과 같이 likelihood를 나타낼 수 있다.
하지만 MLE에서는 계산을 보다 간단하게 하기 위해서 각 관측치에 대한 종속변수가 서로 독립이라고 가정한다.
따라서 2,3번째 줄과 같이 곱셈 형태로 나타낼 수 있다.
• 기본 가정 : MLE의 기본 가정으로는 종속변수가 특정한 확률 분포를 따른다고 가정한다.
• Likelihood can be expressed using the probability distribution(s) used to generate the observed data
• Likelihood is a function of parameters that we want to estimate, which represent the relationship between Xs and y.
Because it is determined by the probability distribution, which is a function of parameters.
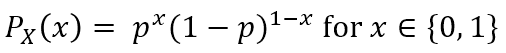
• 각 종속변수의 확률 분포에도 '파라미터'가 존재한다. 위 베르누이 분포 식에서 p가 파라미터에 해당된다.
이러한 확률 분포를 통해서 likelihood를 표현하고, likelihood는 이러한 파라미터에 대한 '함수'가 된다.


• likelihood는 서로 다른 변수들의 종속변수에 대한 결합확률을 이용해서 표현한다.
예시) 학습데이터에 n개의 관측치가 있고, y는 종속변수이다.
P(Y1 = y1)은 첫 번째 관측치의 종속변수가 y1 확률을 나타낸다.
likelihood는 아래와 같이 계산된다.
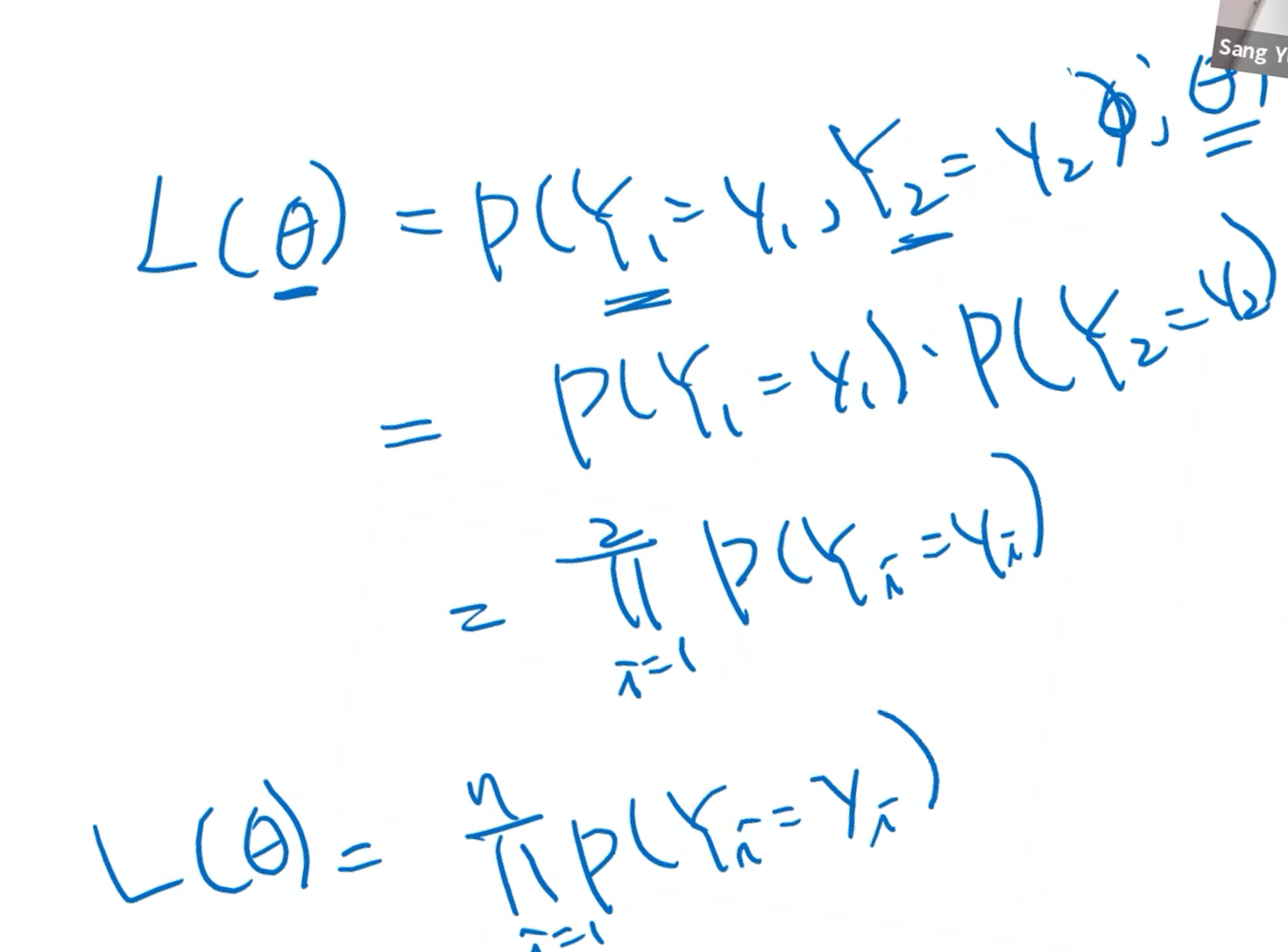
만약 종속변수가 이산변수이고 0or1 값을 취하는 베르누이 분포인 경우
위의 마지막 식을 이어서 표현하면
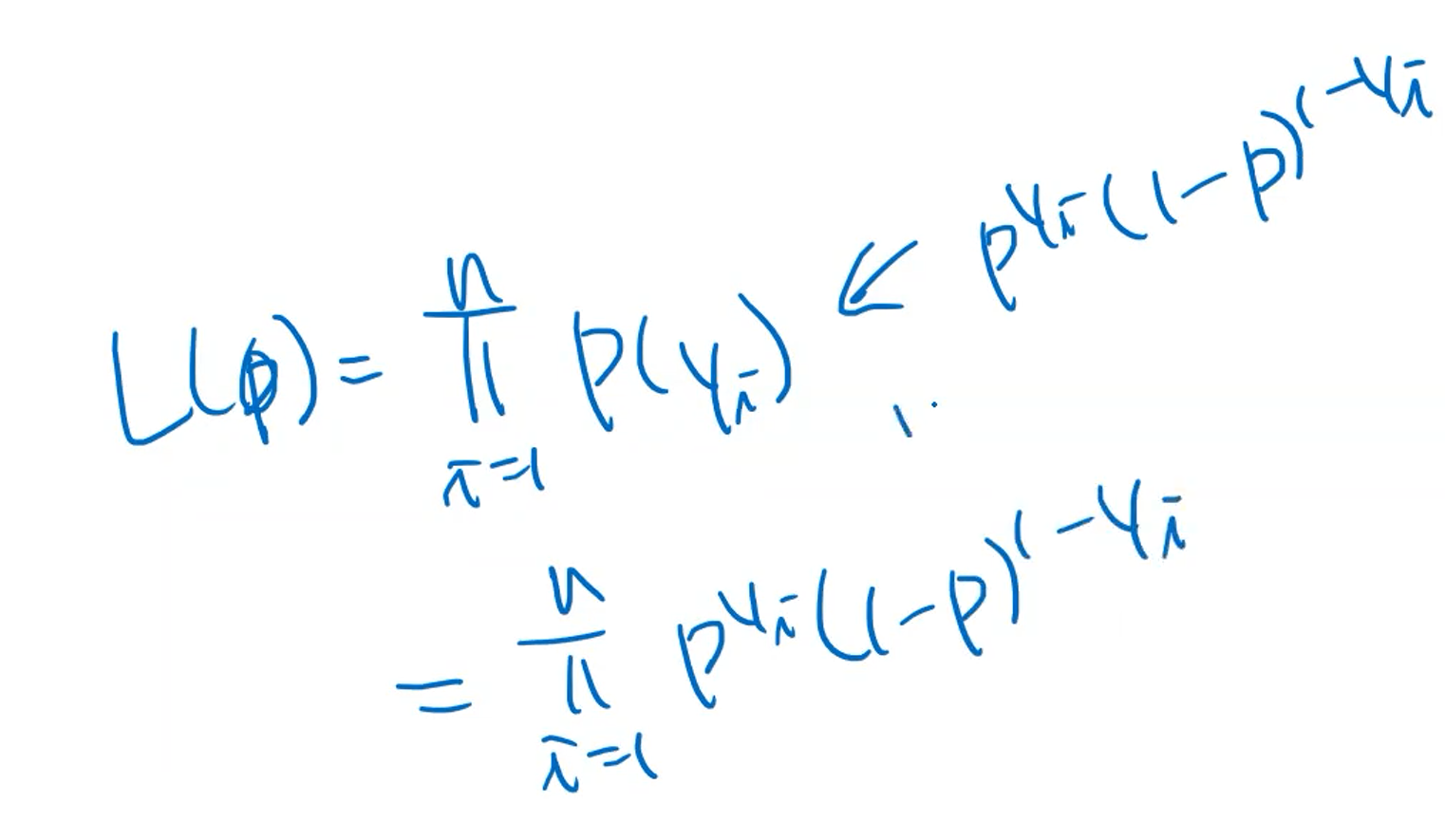
즉 위의 식이 종속변수가 베르누이 분포일 경우에, 해당 종속변수에 대한 likelihood가 된다.
마지막 줄의 P(Yi = yi) 부분이 이산변수인 경우에는 PMF로, 연속변수인 경우에는 PDF로 표현된다.
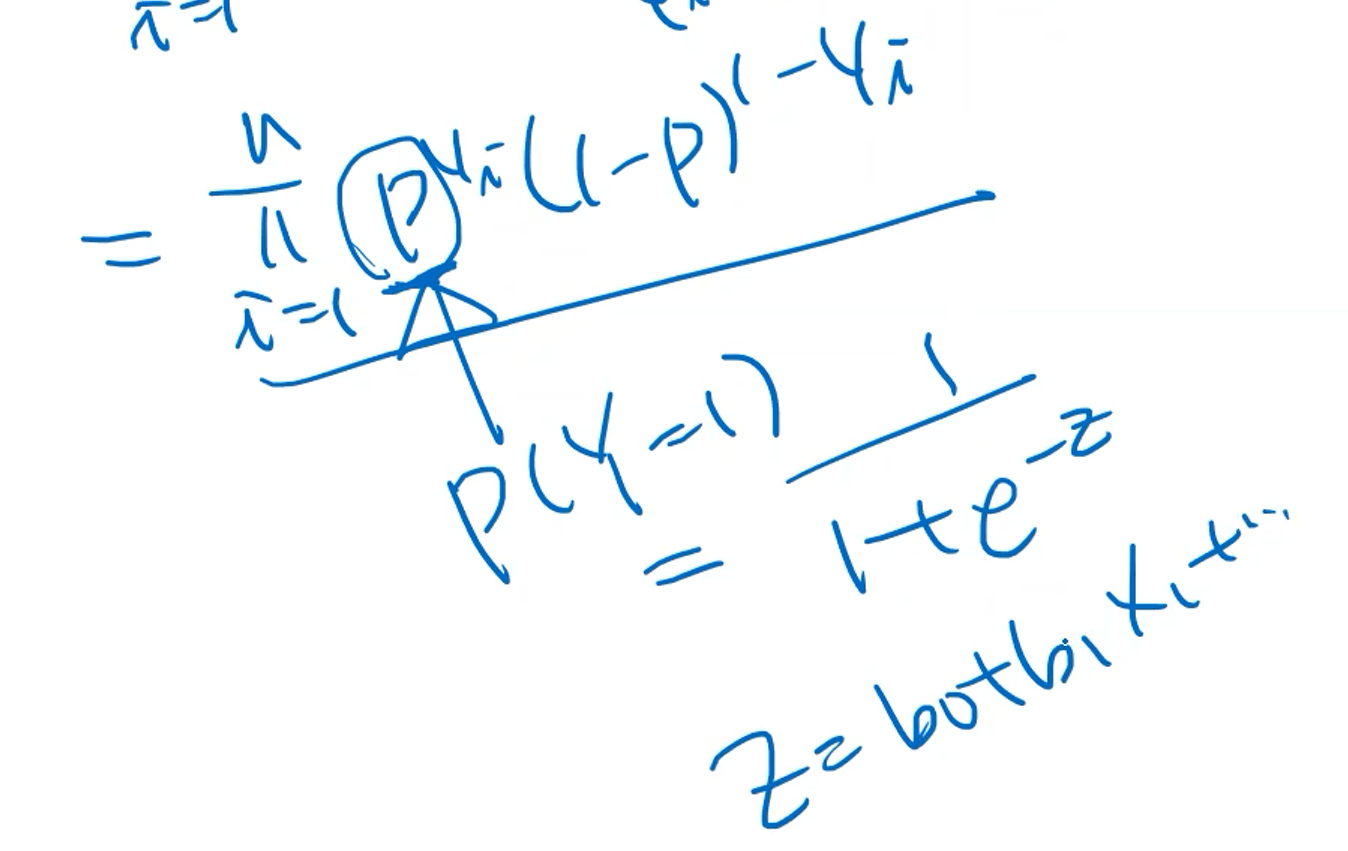
likelihood 함수의 p를 로지스틱 회귀를 나타내는 식으로 자세하게 풀어서 쓰면 위와 같다.
(=p가 베르누이 분포이므로 베르누이 분포의 pmf를 이용해서 표현한다)
따라서 우리가 관심이 있는 식은 결국 독립변수와 종속변수의 관계를 정의하는 b0, b1.... 에 대한 식의 형태로 표현된다.
위 그림에서 가장 처음 식은 위로 볼록한 convex형태인데, 미분을 통해서 최대 지점을 구할 수 있다.
하지만 곱셈 형태에서는 미분이 어려우므로 로그를 취해서 더하기 형태인 log-likelihood로 변환한다.
로그 함수는 단순 증가함수이기 때문에, likelihood와 log-likelihood를 최대화 하는 파라미터 값은 동일하다.
따라서 미분 편의를 위해서 주로 log-likelihood가 많이 사용된다.
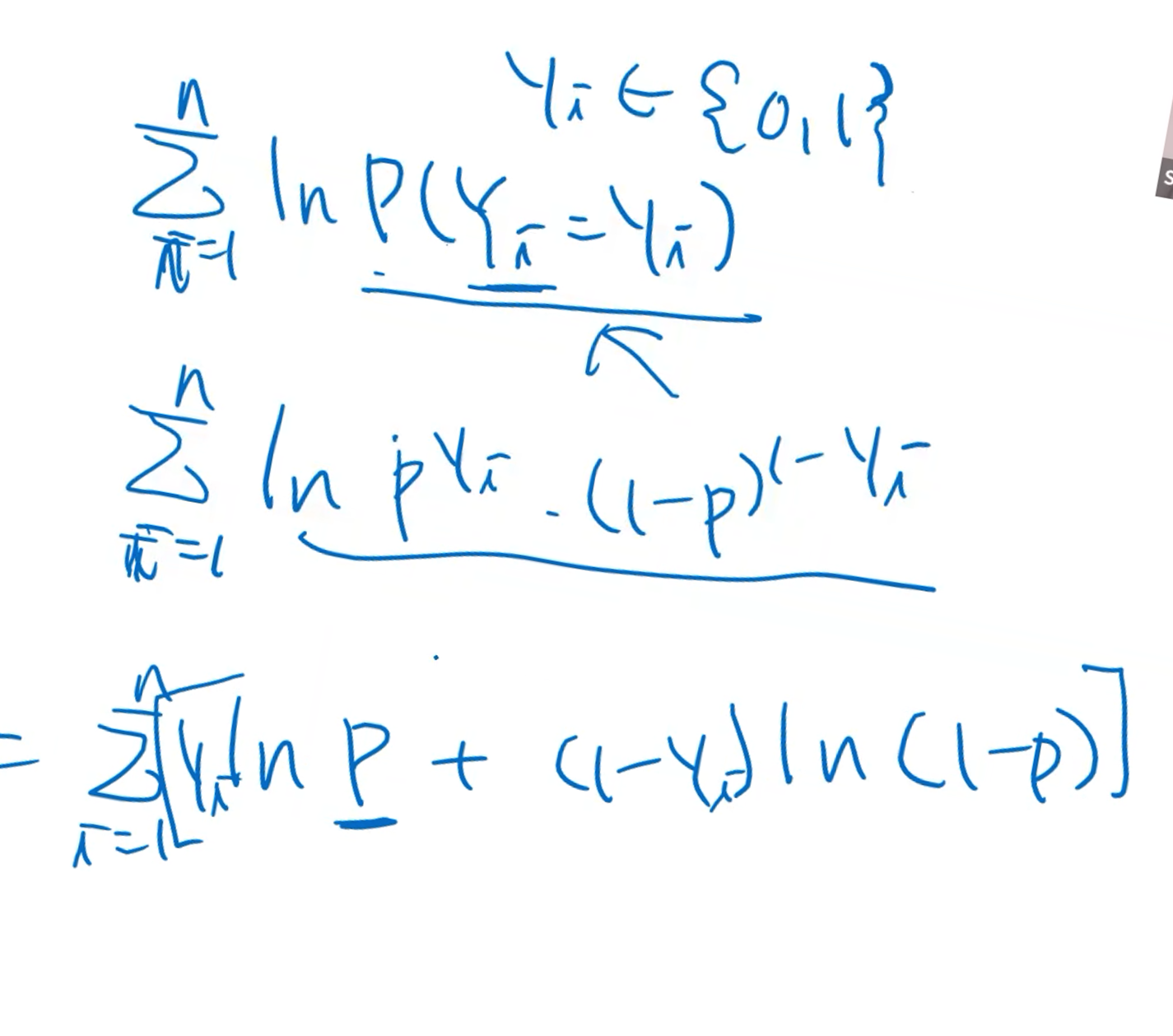
파이 기호는 곱하기를 의미하므로 로그를 취하면 시그마로 바뀐다. 이 형태는 크로스 엔트로피 함수와 동일하다. (부호만 다르다)
여기서 p는 베르누이 분포에서 y=1일 확률을 의미한다.
로지스틱 회귀의 경우 위의 log-likelihood를 최대화 하는 파라미터 p 값을 구하게 되고, 이 과정을 MLE 라고 한다.
하지만 실제 머신러닝에서는 위의 크로스 엔트로피 함수를 손실함수로 사용하고, 손실함수는 그 값을 최소화 해야 한다. 따라서 log-likelihood 식 앞에 마이너스를 붙여서 최소화 문제로 변환하여 사용한다. 마이너스를 붙이게 되면 cross entropy function과 동일하다.
📚Reference
이상엽, 연세대학교 언론홍보영상학부 부교수, 22-1학기 기계학습 이론과 실습
'데이터 분석 > 통계, 분석기법' 카테고리의 다른 글
| 교차 엔트로피(Cross Entropy) (0) | 2022.04.11 |
|---|---|
| 확률 기본 개념 (0) | 2022.03.28 |
| Association Rules - 장바구니 분석 (0) | 2021.11.24 |
| 생존분석(Survival Analysis) : Kaplan-Meier / Cox Proportional Hazard / BYTD (0) | 2021.11.15 |
| VAR (Vector Auto Regressive) 모형 (0) | 2021.11.01 |


댓글