◈ 딥러닝 기본 개념 설명 - 비용함수/경사하강법/규제
✅ 비용함수(Cost Function), 손실함수(Loss Function)
• 비용함수 : 학습데이터에 존재하는 전체의 에러 정도를 의미함. 즉 모델이 설명하지 못하는 정도를 나타냄
따라서, 파라미터의 최적 값은 비용함수의 값을 minimize 하는 값이라고 볼 수 있다.
대표적인 비용함수에는 MAE, MSE, RMSE가 있다.

✔ Normal Equation(정규방정식) :
비용함수가 아래로 볼록한2차 방정식 형태(convex form)인 경우, 미분해서 기울기가 0인 지점을 계산하면 비용함수를 최소화하는 지점을 찾을 수 있다. 하지만 이러한 형태로 비용함수가 나타나는 경우는 드물다. 실제 딥러닝의 비용함수는 우측과 같은 형태로 복잡하게 나타난다.


✔ 경사하강법(Gradient Descent)
따라서, 대부분이 딥러닝 비용함수에서는 Normal Equation을 사용할 수 없기 때문에 경사하강법을 사용함.
한번에 최적의 비용함수 감소 지점을 찾을 수 없기 때문에, 임의의 지점에서 시작해서 값을 업데이트해 가면서 비용함수를 minimize하는 지점을 탐색하는 방법.
✔ 하이퍼 파라미터 (Hyper Parameter)
컴퓨터가 아니라 사람이 지정하는 파라미터. 대표적으로 학습률(Learning Rate)가 있음.
✔ 비용함수 계산 예시 (샘플데이터는 2개, 비용함수 2차함수 형태로 가정)

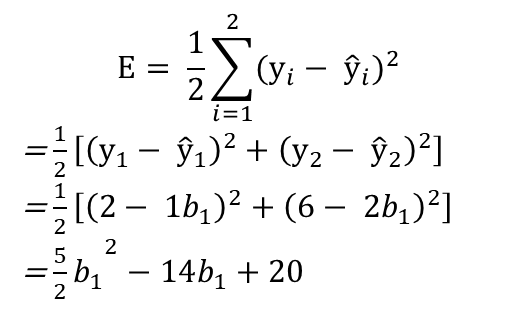

•위의 예시에서 비용함수를 계산하면 아래로 볼록한 이차함수 형태의 비용함수를 도출할 수 있다.

비용함수를 그림으로 나타나면 위와 같다. 일반적으로 딥러닝의 비용함수가 2차함수 형태로 나타나지 않지만, 여기서는 단순화된 샘플을 이용하여 분석한다. 경사하강법은 임의의 b1 값(random)에서 시작하는데 여기서는 15에서 출발한다.

파라미터(b1)을 업데이트하는 식은 위와 같다. 여기서 ∂E/(∂b_1 ) 부분은 b1의 현재값인 (b1, current)에서의 기울기(빨간 직선)를 의미한다. 따라서

와 같은 형태로 나타낼 수 있다. 이 예시에서는 b1=15 에서 시작했으므로 이를 대입해서 계산하면

여기서 η 는 학습률을 나타낸다. 학습률이 크면 한번에 업데이트 되는 값의 크기가 크지만, 비용함수의 최저점으로 수렴하지 못 할 가능성이 있다. 학습률이 작으면 한번에 업데이트 되는 값의 크기가 작지만, 비용함수의 최적화에 많은 시간이 소요된다. η = 0.01인 경우 아래와 같이 계산된다.
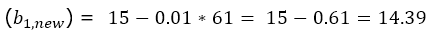
업데이트한 새로운 b1 값은 14.39로 계산되었고, 경사하강법에서는 이 값을 이용해서 다음 최적 값을 계산한다.
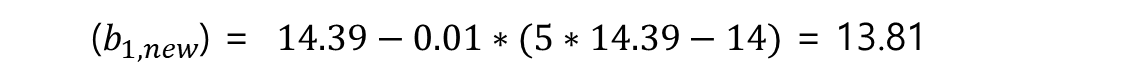
이 과정을 특정 값으로 수렴할 때 까지 반복한다.

액셀에서 이 계산을 계속 반복하다보면 결국 2.8로 수렴하는 것을 확인할 수 있고, 이때가 미분 했을 때 값이 0인 지점과 동일하다.

η = 0.1 로 변경해서 계산해보면 훨씬 빠르게 2.8로 수렴한다는 것을 알 수 있다. 매우 단순한 예제에서도 최적 값을 구하는 단계의 차이가 많이 나기 때문에 실제 모델 학습시에는 파라미터 설정에 따라서 학습 시간이 크게 달라진다는 것을 알 수 있다.
✅ 규제화(Regularization)
• 기존 비용함수를 그대로 사용하면 계수가 큰 파라미터의 영향력이 커지기 때문에 과적합 가능성이 높아진다. 따라서 이를 방지하기 위해서 원래의 비용함수에 penalty term을 추가해서 사용한다.
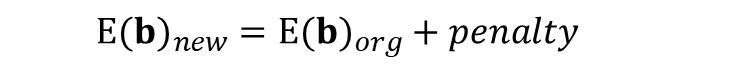
이렇게 penalty를 나타내는 부분을 추가하면, 결과적으로 파라미터의 값이 큰 경우에 패널티가 부여되기 떄문에 비용함수를 최소화하는 과정에서 파라미터의 절대값이 감소한다. 이를 통해서 robust한 모델을 만들어서 과적합을 감소시킬 수 있다. 추가로, 만약 해당 계수의 값이 계속 줄어들어서 0이 되는 경우, 차원이 감소해서 모델이 단순화되는 효과까지 얻을 수 있다(학습에 유용하지 않은 변수는 아예 삭제해버리는 것).
✔ L1 규제

L1 규제의 패널티 텀은 위와 같고, 이를 사용한 비용함수를 식으로 나타내면 ,

✔ L2 규제

L2 규제의 패널티 텀은 위와 같고, 이를 사용한 비용함수를 식으로 나타내면,

여기서 λ(람다)는 학습률과 유사하게 패널티 텀의 영향력을 얼마나 반영할 지를 결정하는 파라미터이다. 위의 예제의 비용함수에 L2 규제를 추가하고 람다를 0.5로 지정하면 아래와 같이 표현할 수 있다.

이 때 비용함수를 최소화하는 파라미터 b1의 값은 14/6으로 패널티 텀이 없을 때 보다 파라미터의 계수가 작아진 것을 확인할 수 있다. 패널티 텀의 λ를 1/2가 아니라 1로 수정하면 파라미터 계수가 14/7로 더 작아진다. 이를 통해서 과적합 가능성을 줄일 수 있다.
✔ L1 vs L2 차이
| L1 규제 | L2 규제 | |
| 공통점 | -파라미터의 크기를 감소시킨다 | |
| 차이점 | -파라미터의 크기가 줄어들어서 0까지 감소함 -피쳐 수가 줄어들기 때문에 모형이 단순해짐 |
-파라미터의 크기가 줄어들지만 0까지 감소하지는 않음 |

원래 비용함수는 검정색 곡선이고 패널티 텀은 붉은색으로 표시됨.
◈ Reference
• 연세대학교 디지털사회과학센터(CDSS) 파이썬을 활용한 딥러닝 기초 워크샵, 이상엽 교수님
'머신러닝, 딥러닝 > 딥러닝' 카테고리의 다른 글
| CNN 사전학습 모델 - LeNet / AlexNet / VGGNet / InceptionNet / ResNet / DenseNet / MobileNet / EfficientNet (0) | 2022.01.17 |
|---|---|
| RNN(순환신경망) 기본 (0) | 2022.01.14 |
| CNN(합성곱 신경망) 기본 (0) | 2022.01.13 |
| 딥러닝 기본 개념 - 신경망 구조, 활성화 함수, Optimizer (0) | 2022.01.11 |
| 딥러닝 기본 용어 정리 (0) | 2021.10.25 |




댓글