Matching & Weighting

📚 Matching

✅ 개요

Korea Summer Workshop on Causal Inference 2022

 treatment 그룹과 control 그룹의 특성을 유사하게 만들어서 비교하는 방법

 

• 매칭과 회귀분석은 사실상 같은 역할을 하지만, 매칭은 회귀 분석과는 다르게 오차와 통제변수 사이의 특정한 functional form을 가정하지 않는다. 

 

 

✅ Propensity Score Matching (PSM)

Korea Summer Workshop on Causal Inference 2022

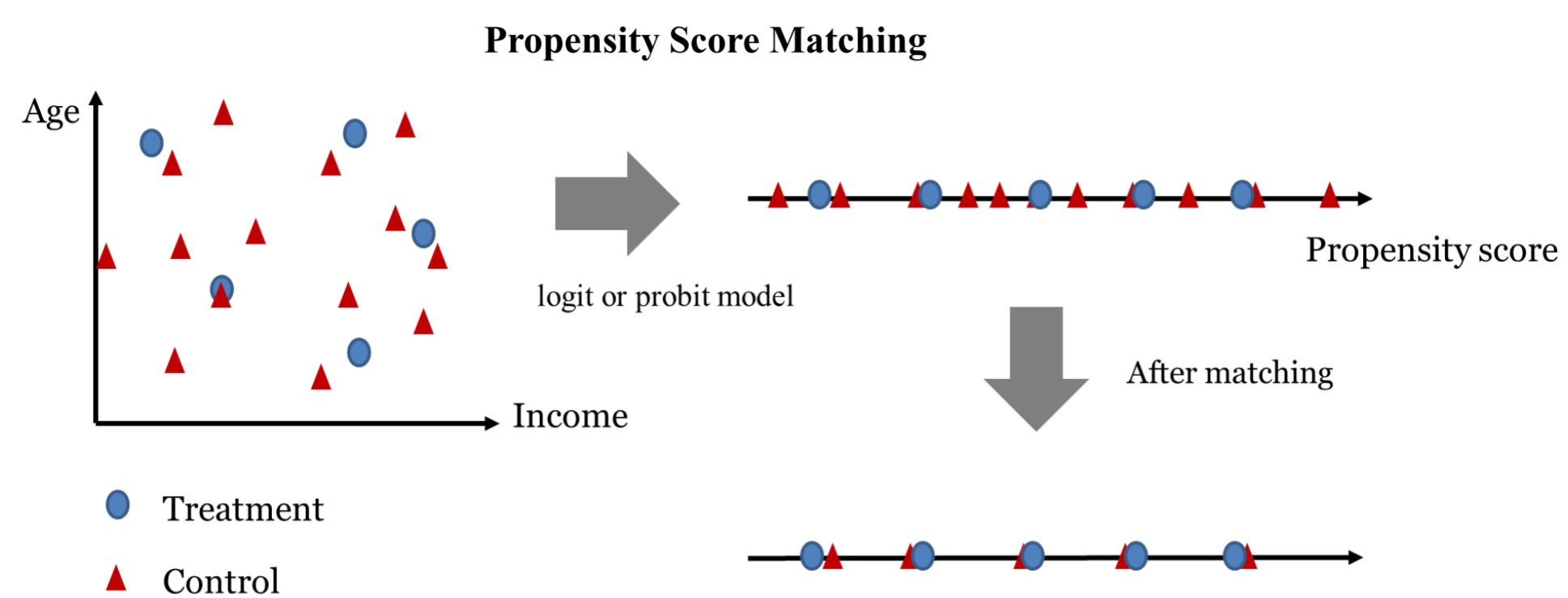
통제 변수가 주어진 상태에서 treatment를 받을 확률을 propensity score라고 한다. treatment 그룹과 control 그룹의 관측치 각각에 대해서 propensity score를 계산하고, 이 값이 비슷한 데이터끼리 매칭하는 방법이 PSM 이다. 

propensity score는 종속변수를 treatment 여부로 두고 logistic regression 또는 probit regression 을 돌려서 구할 수 있다. 

매칭 방식은 관찰 가능한 통제변수로 treatment를 받을 확률을 모두 설명할 수 있다는 강한 가정을 기반으로 한다. 

 

하지만 여기서 사용하는 로지스틱/프로빗 회귀는 이진 분류에 많이 사용되기 때문에 편의상 사용하는 것이다. 실제로는 관찰되지 않은 다양한 변수가 있기 때문에3 propnesity score가 어떻게 계산될지는 알 수 없다. 

 

 

✅ Coarsened Exact Matching (CEM) 

Korea Summer Workshop on Causal Inference 2022

  단순하게 통제 변수들이 비슷한 관측치끼리 매칭하는 방법이다. 정확하게 통제 변수가 같은 관측치 쌍을 찾아서 비교하는 것이 이상적이지만 현실적으로 어렵기 때문에, CEM 에서는 몇 개의 구간(bin)으로 나눠서 보다 느슨한 기준으로 비슷한 데이터를 찾아서 매칭한다. 단 CEM은 데이터 샘플의 수가 줄어든다는 단점이 있다 

 

현재 연구에서는 PSM와 CEM 방법을 둘 다 골고루 활용한다. 반드시 어느 방법이 우월하다고 할 수는 없음. 

 

 

---

📚 Weighting 

✅ 개요

https://towardsdatascience.com/solving-simpsons-paradox-with-inverse-probability-weighting-79dbb1395597

 경우에 따라 매칭이 사용 불가능한 경우에 웨이팅이 유용하게 사용될 수 있다. 매칭은 propensity score가 유사한 데이터끼리 매칭하지만, 웨이팅은 propensity score의 역수만큼을 각 관측치의 가중치로 부여한다. 즉 treatment를 받을 확률이 작은 그룹에는 더 많은 가중치를 부여해서 확률을 높이고, treatment를 받을 확률이 높은 그룹에는 가중치를 적게 부여한다.  이를 통해서 treatment를 받을 확률을 동일하게 만든다. 이 가중치를 Inverse Probability Weighting(IPW)라고 한다. 

 

Korea Summer Workshop on Causal Inference 2022

 위 그림에서 C는 통제변수, X는 독립변수이고 둘 다 0 or 1 값을 가진다고 가정하자. 

통제변수(confounder)를 고려하지 않고 Y에 대한 X의 영향을 확률로 표현하면 우측 식과 같이 나타낼 수 있다. 

Korea Summer Workshop on Causal Inference 2022

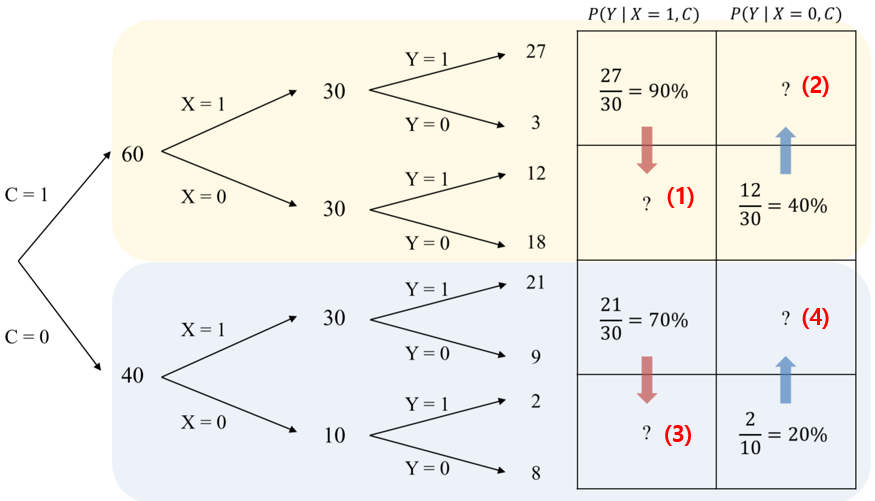
위 그림에서 화살표 방향으로 물음표인 부분은 conterfactual 이기 때문에 실제로는 관측할 수 없다. 

잠재 결과 프레임워크의 주요 가정에 따르면 통제 변수를 이용해서 모든 selection bias를 컨트롤 할 수 있다. 위 그림에서 노란색 그룹은 C=1, 파란색 그룹은 C=0 인 부분인데, 통제변수가 같기 때문에 각 그룹 내에서는 seleciton bias가 존재하지 않아서 비교가 가능하다. 

 

(1) 부분 : X=1 인 경우에 대한 conterfactual인 X=0인 경우이다. 즉  X=1인 경우에 Y=1일 확률은 90%인데, selection bias가 없기 때문에 X=0인 경우에도 이 확률이 동일하게 90%라고 가정한다. 따라서 아래 그림의 30 * 0.9 =27 / 30 * 0.1 =3 이 된다. 

 

(3) 부분 : X=1 인 경우에 대한 counter factual이며, X=1인 경우에 Y=1일 확률이 70% 이기 때문에 마찬가지로 (3) 에서도 이 확률이 동일하게 70%일 것이라고 가정한다. 따라서 30 * 0.4 = 12 / 30 * 0.6 = 18 이 된다. 

Korea Summer Workshop on Causal Inference 2022

앞선 가정에 의해서 가상의 conter factual을 만들면 이것을 pseudo-population 이라고 한다. 여기서 treatment와 conterfactual을 비교하면 causal effect를 파악할 수 있다. 

 

위 과정은 통제 변수가 주어진 상황에서 treatment를 받을 확률인 propensity score의 역수를 곱하는 것과 동일한 의미를 가진다. 아래 그림으로 살펴보면 

Korea Summer Workshop on Causal Inference 2022

 

따라서 pseudo population을 생성할 경우에 아래와 같이 통제변수=1 인경우에 X=1 또는 0 일 확률이 동일하다. 위 그림에서는 60개 : 60개이다. 마찬가지로 통제변수=0 인 경우에도 40개 : 40개로 X =1 또는 0 일 50%이다. 

즉 통제변수에 상관없이 treatment (=X)를 받을 확률이 50대 50으로 동일하게 되고, random assignment와 동일한 형태가 된다. 

 

---

📚  Regression vs Matching vs Weighting 

Korea Summer Workshop on Causal Inference 2022

 회귀에서는 통제변수의 값을 고정한다. 매칭의 경우에는 통제변수의 값이 동일하도록 통제변수를 고정한다. 즉 회귀와 매칭은 통제변수가 selection bias를 설명한다는 가정 하에서 통제변수를 조정함으로써 selection bias를 해결하고자 한다.

 

 반면 웨이팅은 통제변수와 상관없이 treatment를 받을 확률이 50대50으로 random assignment와 유사한 환경이 되도록 pseudo population을 구성한다. 위 그림에서도 보는 것처럼 통제변수 Z에서 독립변수 A로 가는 화살표를 아예 제거하는 방법이다. 상황에 따라서 conditioning 방식을 사용할 수 없는 경우에는 웨이팅을 사용할 수 있다. 

 

<회귀>

단점 :

• 통제변수가 selection bias를 설명한다고 가정하지만 구체적인 정도를 데이터로 검증할 수 없다. 이 부분은 이론을 통해서 설명할 수 밖에 없다. 

 

<매칭>

장점 : 

• 매칭 후에 두 그룹의 통제변수 값을 살펴보면서 잘 되었는지 직관적으로 비교할 수 있다. 

단점 : 

• 샘플 사이즈가 줄어들기 때문에 통계적인 추정이 비효율적이 된다. 원래 데이터와 매칭된 데이터의 특성이 많이 달라질 경우에는 매칭된 데이터에서 나타나는 treatment effect를 원래 데이터에 적용하지 못할 수도 있다. 

 

<웨이팅>

장점 : 

• 매칭과 달리 데이터를 전부 살리고 추가적인 데이터를 웨이팅해서 사용하기 때문에 매칭의 단점을 보완할 수 있다. 

• conditioning이 불가능한 상황에서 사용할 수 있다. 

단점 : 

• propensity score를 정확하게 추정할 수 있을 때에만 사용할 수 있다. 

 

 

 하지만 위 모든 방법들은 관찰된 변수로 selection bias를 통제할 수 있다는 것을 가정으로 한다는 것을 반드시 기억해야 한다. 따라서 관찰되지 않은 변수의 영향력이 적다는 것을 설득력있게 주장하거나, 관찰된 변수들을 이렇게 잘 고려하면 관찰되지 않은 변수들의 영향도 효과적으로 통제할 수 있다는 것을 설득해야 한다. 대부분의 경우 회귀/매칭/웨이팅은 다른 방법론과 함께 사용되는 경우가 많다. 

 

---

📚  Reference

• Korea Summer Workshop on Causal Inference 2022, Boot Camp for Beginners, 매칭과 역확률가중치

 

https://www.youtube.com/watch?v=BVBUQz3Ix8w&list=PLKKkeayRo4PV_6-nbBgmUNOSpG1OO49M3&index=7